Принцип работ, функции, алгоритм систем правления с отрицательной обратной связью, страница 3

                                                                                  Δx=A

                                                 x₀                                                 t′

                                                                                                      t

Для описания ступенчатого воздействия используют специальную функцию – функцию ХЕВИСАЙДа. Это единичная, ступенчатая функция 1(t).

              0, t<0

1(t)=

              1, t>0    Данная функция позволяет математически записать ступенчатое воздействие с любым законом изменения.

x(t)                                                           x(t)

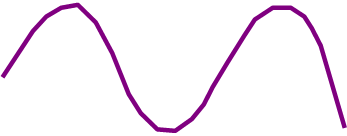                          x(t)=sin ωt                                         x(t)=1(t)*sin ωt

 

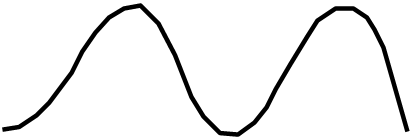
                                                        t                                                                t

 

          x(t)

                          x(t)=1(t)

                                                         t

Построим график обычной синусоидальной функции Аsin ωt, где ω- скорость с которой единичный вектор вращается против часовой стрелки.

Р/м геометрическую интерпретацию (модель) синусоидальной и косинусоидальной зависимостей, построим декартовы координаты (оси 90⁰) и р/м вектор длиной 1 (модуль вектора равен 1 ), который вращается с угловой скоростью ω= 2π f против часовой стрелки.

1) при t=0, вектор направлен по оси х (вещественной оси), представим что вектор вращается по часовой стрелке и в момент t вектор повернется на угол α=ωt, проекции вектора на вещественную ось будет 1*cos α (если длина вектора А, то проекция будет равна А* cos α), проекция вектора на мнимую ось будет равна 1*sin α. Вектор в каждый момент времени t занимает новое положение и его проекция на ось Im  (минимая ось)   изменяется по закону  sin.

Если построить график зависимости проекции на минимую ось от времени , то получим известную нам синусоидальную зависимость. Обратим внимание, что по оси t графики синуса могут быть отложены 2 параметра( координаты):

                                                                                                            2                                                                                                            Im

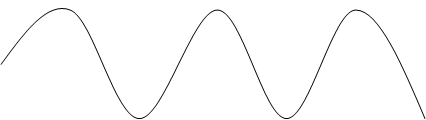           2                   6                        t₀……сек                       1*sin ωt

                3                    7                                                                                                             1

                                                                                           3                                        Re                                          

                            5                  9                                                                                                           α= ωt

        π/2                                                     α= ωt

                     4                  8                     4

f- количество периодов в 1 сек.    T=1/f                       ω= 2πf

                                                         x(t)=A* sin(ωt)

Мы р/м вращение единичного вектора. Если синусоида имеет амплитуду А, вращается не единичный вектор, а вектор длиною А.

2) в электрических схемах, СУ и других системах, по аналогии могут рассматриваться несколько вращающихся векторов, сдвинутых один относительно другого на несколько углов, например : x₁ =A₁* sin(ωt)

                                                 х₂ =A₂* sin(ωt+φ)             ω             А₂

 

                                                                                                           А₁

                                                                                                           Φ

Это означает, что при t=0 вектора А₁ и А₂ сдвинуты один относительно другого на угол  φ. Соответственно на временном графике мы имеем 2 синусоиды:

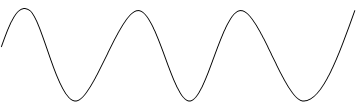
                                              х₂ =A₂* sin(ωt+φ)           Вывод:                    при аргументе

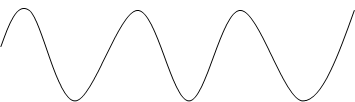                                                                                      (…+φ) функция смещается влево,

                                                                                      т.к. угол  при  t=0  уже имеет

                                                                                      значение φ.

                                                          x₁ =A₁* sin(ωt)

x(t)=[ 1(t)-1(t-τ)] t²

Алгоритм построения:

1)  строим график основной функции t², в данном случае - парабола, но закон изменения сигнала может иметь любой вид: ступенчатый, линейный, синусоидальный и др.

                x(t)                      x(t)=t²

                                         t

2)  строим график функции, заключенной в квадратные скобки 1(t)-1(t-τ)- это сумма

     двух графиков функций  1(t)  и  1(t-τ) , где 1(t)- единичная функция хевисайда,

     принимающая значение 1 в момент t=0, или 1(t-0)=1(t), следовательно   -1(t-τ)

     включается при t=τ (по аналогии) и её значение равно –1. Сумма двух графиков

     получается суммированием ординат графиков функций 1(t)  и  1(t-τ)  при

     различных значениях t. Т.о. 1(t) - 1(t-τ) означает импульсная амплитуда, которая

     включается в момент t=0 и выключается в момент t=τ.

            x(t)                                       x(t)                                x(t)

                                     1(t)                           1(t-τ)                                 1(t)-1(t-τ)

                                          t                                            t                                    t