Оцифровывание. Теория квантования. Теория дискретизации по времени

 4.5.2 Оцифровывание

   Как мы увидели выше, на входе процессора в системе сбора данных должен осуществляться перевод аналогового сигнала в цифровой вид, то есть сигнал должен быть преобразован таким образом, чтобы он стал дискретным по времени и квантованным по величине. Другими словами, аналоговый сигнал необходимо преобразовать в поток двоичных слов , соответствующих моментам взятия выборок .Обычно эти слова поступают на вход процессора параллельно, то есть в виде одного полного слова на каждую выборку. При преобразовании аналогового сигнала в последовательность чисел вносятся ошибки и искажения. На рис. 4.16 показано возникновение этих ошибок во временной области и по величине для аналогового входного сигнала (t), Из-за погрешности в моментах взятия выборок  возникает ошибка по величине, которая зависит от того, насколько «круто» изменяется сигнал(t). По мере роста высокочастотных компонент в сигнале(t) эти ошибки становятся все больше. Если бы этих ошибок не было вовсе, то аналоговый эквивалент двоичного сигнала D выглядел бы как на рис. 4.16. В действительности, меняется в пределах полосы, ограниченной на рис. 4.16 штриховыми линиями.

   Таким образом, ошибка равна:

.

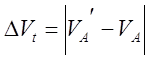   Эта (полная) ошибка , больше, чем , и определяется ошибками квантования, погрешностями аналого-цифрового преобразования и ошибками, возникающими при взятии выборок, вдобавок к погрешностям в задании точек дискретизации на оси времени. В следующих разделах мы рассмотрим порознь ошибки, возникающие в результате квантования и при взятии выборок.

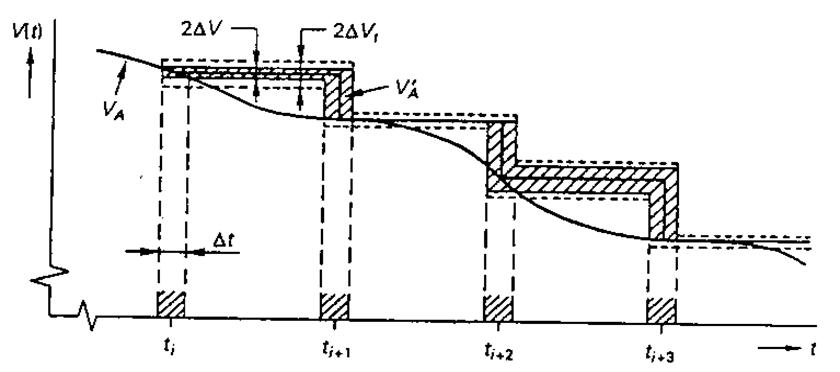
Рис. 4.16. Ошибки, возникающие при преобразовании аналоговою сигнала.– значение сигнала, восстановленного после преобразования.

4.5.3 Теория квантования

 Даже если предположить, что взятие выборок и аналого-цифровое преобразование выполняются идеально (т.е. без ошибок), то все равно нам придется иметь дело с ошибками квантования (см. раздел 3.3.6). На рис. 3.63(Ь) эта ошибка была показана для случая, когда входной сигнал  линейно нарастает. Таким образом, ошибка квантования равна:

Q=,

где– аналоговый эквивалент двоичного выходного сигнала на выходе АЦП. Так как двоичное слово D = () содержит n +1 битов, наименьшее приращение равно: .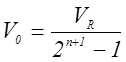

   Аналого-цифровой преобразователь на рис. 3.63 вносит так называемую «ошибку округления». При таком квантовании максимально возможная ошибка определяется неравенствами: .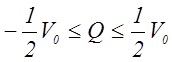

   Следовательно, максимальная ошибка квантования при округлении равна плюс или минус половине значения единицы в младшем разряде. При усечении ошибка квантования лежит в пределах .

  Объединяя все эффекты квантования на пути следования сигнала в системе сбора данных, мы можем представить их как результат действия одного блока, назвав его «устройством квантования». Приведенными выше соотношениями описывается нелинейная модель такого устройства квантования как в случае округления, так и при усечении. На рис. 4. 17 мы снова обратимся к ошибкам, возникающим при округлении. При таком подходе мы сталкиваемся с проблемой, состоящей в том, что нелинейность трудно описать аналитически. Поэтому часто пользуются стохастической моделью, представленной на рис. 4.17(d). Согласно этой модели устройство квантования содержит источник аддитивного шума квантования; выходной сигнал равен сумме входного сигнала и шума квантования .Шум квантования имеет плотность распределения вероятностей f(Q), изображенную на рис. 4. 17(е). Считается, что Q равновероятно принимает все значения между + / 2 и - / 2; распределение вероятностей является равномерным. Среднее значение  равно нулю, а дисперсия определяется соотношением: 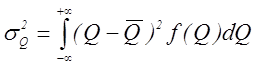 и равна .

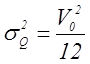    Таким образом, среднеквадратическое значение (стандартное отклонение) добавляемого шумового сигнала равно:

 = .

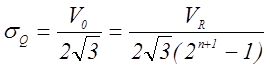   Отношение сигнал/шум (SNR), как следствие ошибки квантования, в случае синусоидального сигнала с пиковым значением  () равно

SNR=.

    Это соотношение иллюстрируется графиком на рис. 4.18, где отношение сигнал/шум SNR указано в логарифмическом масштабе (в дБ). Из графика ясно видно, насколько важно подавать на вход АЦП возможно больший сигнал (наибольший, при котором еще не происходит ограничения). Мы видим также, что при увеличении разрешающей способности АЦП на 1 бит значение SNR растет на 6 дБ.

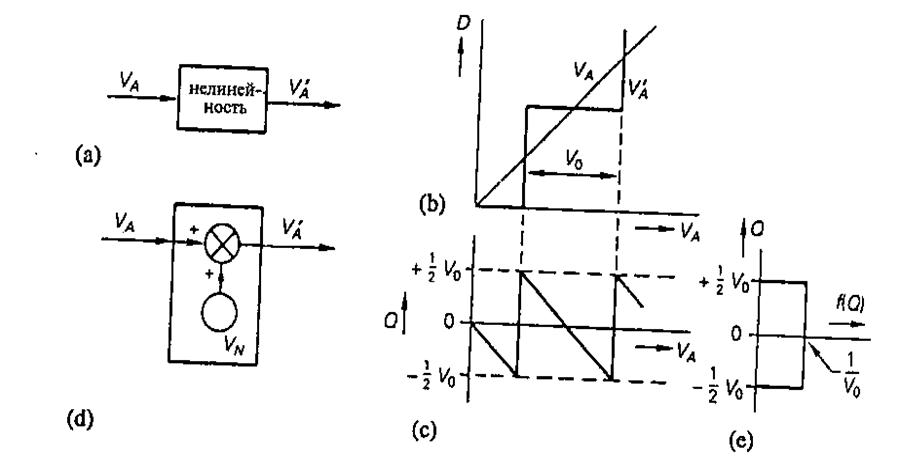
Рис. 4.17. Устройство квантования с источником шума квантования на пути следования сигнала в системе сбора данных, (а) Устройство квантования как нелинейный элемент с характеристикой, изображенной на рис. (Ь), и ошибкой квантования Q, показанной на рис. (с), (d) Стохастическая модель устройства квантования. Добавляемый шум имеет плотность распределения вероятностей, приведенную на рис. (е).

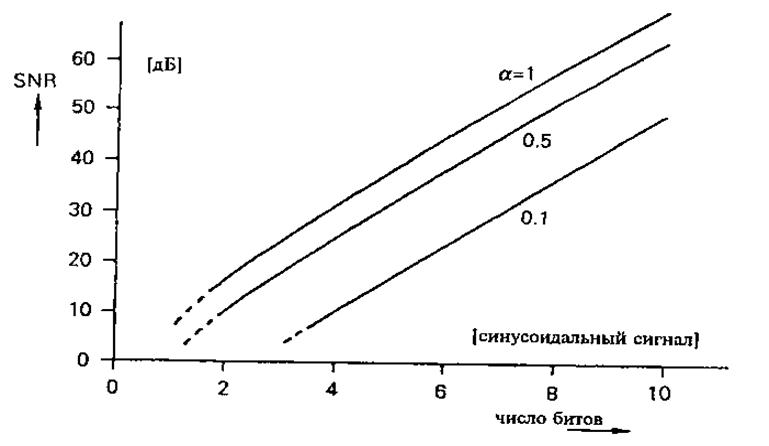
Рис. 4.18. Влияние шума квантования на отношение сигнал/шум SNR.on« синусоидального сигнала с амплитудой, составляющей -ю часть максимального сигнала на входе АЦП.

     Шум квантования в АЦП не является единственным источником ошибок квантования в системе сбора данных. Цифровой процессор обрабатывает сигнал, оперируя только со словами конечной длины. Из-за этого также возникают ошибки квантования (которые становятся совсем большими, когда применяется процессор «с фиксированной запятой»). Это легче всего продемонстрировать на примере простого цифрового перемножения. Цифровой входной сигнал поступает на вход процессора от АЦП с ошибкой квантования (со стандартным отклонением ). В процессоре этот сигнал умножается на число ,которое получено в результате вычислений и потому также представляется словом конечной длины. Это число содержит ошибку квантования (со стандартным отклонением ). В результате перемножения получаем число:

.

    Если предположить, что два источника шума квантования не коррелированны ни друг с другом, ни с самими сигналами  и, то по гауссовому правилу распространения ошибок (см. раздел 2.3.2) находим:

.

     Пренебрегая малыми членами, получим: .

    Результатом перемножения будет выходной сигнал в форме слова конечной длины. Производимое при этом усечение эквивалентно добавлению на выходе перемножителя шума квантования со стандартным отклонением. Поскольку этот источник шума можно считать независимым по отношению к двум источникам, упоминавшимся ранее, мы можем результирующую дисперсию представить в виде:

.

    Длина слов, которыми представлены участвующие в этом примере переменные, не обязательно должна быть одинаковой. Поскольку соответствующие плотности распределения вероятностей являются равномерными, дисперсия каждой из этих переменных равна (1/12) (LSB), где LSB – значение единицы в младшем разряде. Вот почему важно, чтобы число перемножений при обработке сигнала было возможно меньшим и сами перемножения располагались возможно ближе к месту получения конечного двоичного результата.