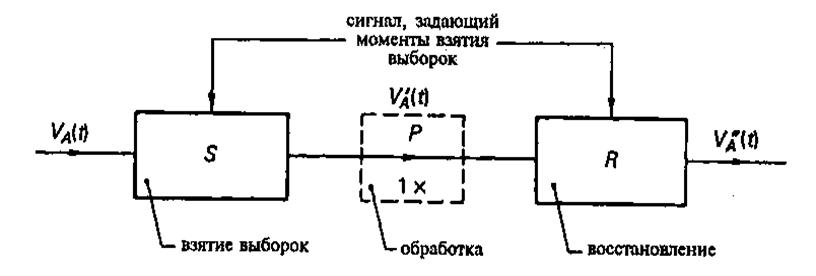
Рис. 4.26.
Восстановление как операция, обратная взятию выборок: ![]()
В блоке, помеченном символом S,
осуществляется взятие выборок из аналогового входного сигнала ![]() .В блоке, помеченном символом R,
производится восстановление сигнала
.В блоке, помеченном символом R,
производится восстановление сигнала ![]() , представленного
посредством выборок. Если бы мы выполняли взятие выборок и восстановление
идеально, то результат восстановления был бы точной копией входного сигнала:
, представленного
посредством выборок. Если бы мы выполняли взятие выборок и восстановление
идеально, то результат восстановления был бы точной копией входного сигнала: ![]() .Поэтому идеальное восстановление
представляет собой операцию, в точности обратную идеальному взятию выборок!
Однако в общем случае при выполнении обеих операций вносятся ошибки. Ошибки,
возникающие в результате взятия выборок, рассмотрены в предыдущем разделе.
Чтобы избежать ошибок вследствие наложения спектров, применяется
«предшествующая взятию выборок» фильтрация. На практике такой фильтр всегда
отбрасывает часть полезного сигнала, создавая тем самым «ошибки исключения».
Когда происходит восстановление, также отбрасываются хвосты спектра, выходящие
за пределы основной полосы частот. При этом также вносятся ошибки исключения.
.Поэтому идеальное восстановление
представляет собой операцию, в точности обратную идеальному взятию выборок!
Однако в общем случае при выполнении обеих операций вносятся ошибки. Ошибки,
возникающие в результате взятия выборок, рассмотрены в предыдущем разделе.
Чтобы избежать ошибок вследствие наложения спектров, применяется
«предшествующая взятию выборок» фильтрация. На практике такой фильтр всегда
отбрасывает часть полезного сигнала, создавая тем самым «ошибки исключения».
Когда происходит восстановление, также отбрасываются хвосты спектра, выходящие
за пределы основной полосы частот. При этом также вносятся ошибки исключения.
Из рис. 4.24(а) видно, что ошибки исключения
определяются теми составляющими спектра в окрестности нуля, которые выходят за
пределы интервала ![]() ; они отфильтровываются. В
системе сбора данных возникают также «ошибки включения». Они являются
следствием невозможности полностью отфильтровать на стадии восстановления
компоненты первой копии спектра исходного сигнала. В ситуации, изображенной на
рис. 4.24(а), эта ошибка возникает из-за тех компонент первой копии, которые
оказываются в интервале
; они отфильтровываются. В
системе сбора данных возникают также «ошибки включения». Они являются
следствием невозможности полностью отфильтровать на стадии восстановления
компоненты первой копии спектра исходного сигнала. В ситуации, изображенной на
рис. 4.24(а), эта ошибка возникает из-за тех компонент первой копии, которые
оказываются в интервале![]() . Ошибки
исключения и ошибки включения определяются заштрихованными областями на этом
рисунке. Объединенные вместе эти ошибки образуют полную «ошибку из-за наложения
спектров». Поэтому можно утверждать, что для хорошего восстановления
. Ошибки
исключения и ошибки включения определяются заштрихованными областями на этом
рисунке. Объединенные вместе эти ошибки образуют полную «ошибку из-за наложения
спектров». Поэтому можно утверждать, что для хорошего восстановления ![]() из сигнала, представленного посредством
выборок, мы должны в возможно большей степени уменьшить ошибки исключения и
ошибки включения, стараясь свести их к нулю. Из предыдущего рассмотрения
следует, что посредством «предшествующей взятию выборок» фильтрации можно
сделать «ошибки включения» произвольно малыми. Однако при этом “ошибки
исключения” очень сильно возрастают. И обратно: не применяя вовсе
предварительной фильтрации и фильтрации при восстановлении, можно свести ошибку
исключения к нулю, но тогда будет большой ошибка включения. Таким образом,
следует ожидать, что полная ошибка вследствие наложения спектров будет
минимальной, если удастся найти определенный баланс между ошибками исключения и
ошибками включения. Больше того: можно ожидать, что этот минимум будет
уменьшаться по мере того, как частота взятия выборок будет расти. Чтобы
подвергнуть эти ошибки более пристальному анализу, мы рассмотрим сначала чуть
более подробно несколько методов восстановления.
из сигнала, представленного посредством
выборок, мы должны в возможно большей степени уменьшить ошибки исключения и
ошибки включения, стараясь свести их к нулю. Из предыдущего рассмотрения
следует, что посредством «предшествующей взятию выборок» фильтрации можно
сделать «ошибки включения» произвольно малыми. Однако при этом “ошибки
исключения” очень сильно возрастают. И обратно: не применяя вовсе
предварительной фильтрации и фильтрации при восстановлении, можно свести ошибку
исключения к нулю, но тогда будет большой ошибка включения. Таким образом,
следует ожидать, что полная ошибка вследствие наложения спектров будет
минимальной, если удастся найти определенный баланс между ошибками исключения и
ошибками включения. Больше того: можно ожидать, что этот минимум будет
уменьшаться по мере того, как частота взятия выборок будет расти. Чтобы
подвергнуть эти ошибки более пристальному анализу, мы рассмотрим сначала чуть
более подробно несколько методов восстановления.
На выходе системы сбора данных ЦАП дает ступенчатое приближение к желаемому аналоговому выходному сигналу, как это показано на рис. 4.27(а). Но в моменты времени, когда цифровой сигнал на входе ЦАП изменяется, на выходе могут возникать паразитные кратковременные выбросы напряжения. Поэтому обычно вслед за ЦАП ставят схему выборки и хранения, которая производит взятие выборки тогда, когда переходные процессы на выходе ЦАП заканчиваются. В результате получается ЦАП «с защитой от выбросов».
Нетрудно представить себе, что сигнал, возникающий
на выходе ЦАП с защитой от выбросов, является результатом взятия выборок
входного сигнала в моменты ![]() с последующим
удержанием значения выборки в течение интервала времени
с последующим
удержанием значения выборки в течение интервала времени![]() .
О таком ЦАП говорят как о «схеме фиксации нулевого порядка». Эта схема
осуществляет заполнение (аналогового) выходного напряжения между моментами
взятия выборок. Поэтому ее можно считать восстанавливающим или интерполирующим
фильтром. Можно показать, что передаточная функция
.
О таком ЦАП говорят как о «схеме фиксации нулевого порядка». Эта схема
осуществляет заполнение (аналогового) выходного напряжения между моментами
взятия выборок. Поэтому ее можно считать восстанавливающим или интерполирующим
фильтром. Можно показать, что передаточная функция ![]() этого
фильтра равна:
этого
фильтра равна:
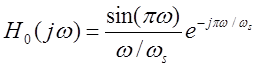 .
.
Здесь![]() – частота взятия
выборок. Чтобы получить передаточную функцию такого фильтра с фиксацией
нулевого порядка, можно воспользоваться схемой, представленной на рис. 4.26,
предположив, что блок S представляет собой идеальное устройство взятия
выборок с использованием
– частота взятия
выборок. Чтобы получить передаточную функцию такого фильтра с фиксацией
нулевого порядка, можно воспользоваться схемой, представленной на рис. 4.26,
предположив, что блок S представляет собой идеальное устройство взятия
выборок с использованием ![]() -функций, а блок R является
схемой фиксации нулевого порядка. На рис.4.28 приведена частотная
характеристика этого восстанавливающего фильтра. Мы видим, что этот фильтр не
вносит фазовых искажений; сдвиг фаз изменяется с частотой линейно.
-функций, а блок R является
схемой фиксации нулевого порядка. На рис.4.28 приведена частотная
характеристика этого восстанавливающего фильтра. Мы видим, что этот фильтр не
вносит фазовых искажений; сдвиг фаз изменяется с частотой линейно.
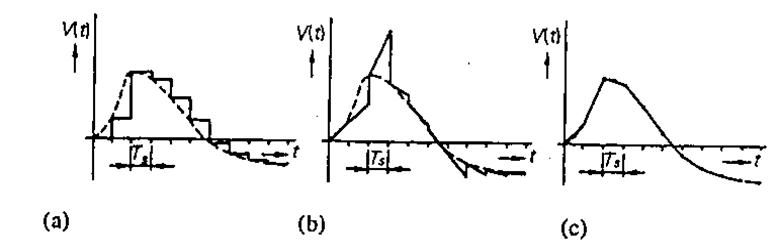
Рис.4.27.(а) Результат работы схемы фиксации нулевого порядка в качестве восстанавливающего фильтра во временной области. (Ь) То же для схемы фиксации первого порядка с предсказанием (с линейной экстраполяцией), (с) То же для интерполирующей схемы фиксации первого порядка (с линейной интерполяцией). NB: На рисунке не показана задержка на один интервал дискретизации, которая имеет место в случае применения последнего метода.
Найдем максимальную мгновенную ошибку, возникающую на выходе такой схемы, для
синусоидального сигнала ![]() . Ошибка будет
максимальной в точках пересечения нуля. В этом месте скорость изменения сигнала
равна
. Ошибка будет
максимальной в точках пересечения нуля. В этом месте скорость изменения сигнала
равна ![]() . Но она равна также максимальной
ошибке
. Но она равна также максимальной
ошибке ![]() , деленной на период
, деленной на период ![]() , с которым берутся выборки.
Следовательно, можно считать, что
, с которым берутся выборки.
Следовательно, можно считать, что ![]() . Тогда
максимальная относительная ошибка по величине равна:
. Тогда
максимальная относительная ошибка по величине равна:
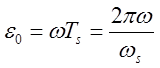
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.