Оцифровывание. Теория квантования. Теория дискретизации по времени, страница 4

Из рис. 4.23 видно, что пока наибольшая частота входного сигнала  остается меньше половины частоты, с которой берутся выборки, мы имеем возможность восстановить из спектра спектр исходного сигнала (выбрать нулевую копию) с помощью фильтра нижних частот. Такой фильтр устраняет все копии, находящиеся на оси частот вне его полосы пропускания. Такие фильтры называют «восстанавливающими» или «интерполирующими» фильтрами. Если бы частота была очень близка к значению, то нам понадобился бы фильтр нижних частот с очень крутым спадом частотной характеристики (с прямоугольной характеристикой). Нельзя построить фильтр с такой характеристикой для работы в «реальном времени». Правда, мы могли бы записать сигнал, и позднее, когда весь сигнал известен полностью, с помощью математических манипуляций восстановить исходный сигнал. Мы создали бы таким образом фильтр, не удовлетворяющий «принципу причинности»; это такой фильтр, в котором используется знание об изменениях входного сигнала в будущем. Поэтому практический вывод таков: пока, мы в состоянии безошибочно восстановить входной сигнал.

   Ситуация становится совсем другой, когда упомянутое условие не выполняется, как это показано на рис. 4.24. Мы видим, что в этом случае копии спектров начинают накладываться друг на друга. При этом уже нет возможности безошибочно восстановить нулевую копию даже при наличии идеального фильтра нижних частот.

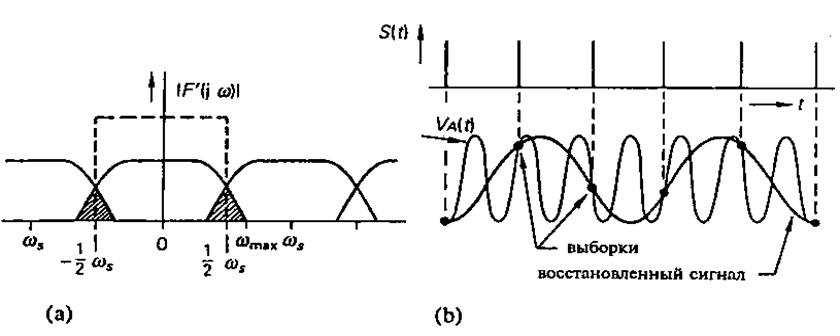
Рис.4.24.(а) Взятие выборок в случае, когда условия теоремы Шеннона о выборках не выполняются. (Ь) Временная диаграмма, отображающая наложение спектров, в случае синусоидального сигнала с частотой. Частота восстановленного сигнала равна .

   На рис. 4.24(b) показано, как выглядит в этом случае результат во временной области. Выборки берутся из синусоидального входного сигнала с частотой. Пытаясь восстановить исходный сигнал, мы пропускаем выборки через фильтр нижних частот с частотой среза. В результате получаем синусоидальное колебание той же самой амплитуды, что и исходный сигнал, но с частотой. Это очевидно также из графика на рис. 4.24(а), где изображен спектр сигнала, представленного посредством выборок. Вся мощность сигнала сосредоточена по существу в составляющей, являющейся зеркальным отражением исходного сигнала относительно частоты. Ошибки, возникающие из-за перекрытия копий спектра сигнала в заштрихованных областях, называют «ошибками вследствие наложения спектров». Из рис. 4.24(а) следует, что можно избежать ошибок вследствие наложения спектров, если до взятия выборок пропустим входной сигнал через фильтр нижних частот.

   Такой фильтр, осуществляющий «предварительную фильтрацию», ослабляет высокочастотные составляющие в спектре сигнала, уменьшая тем самым, или даже исключая вовсе, ошибки вследствие наложения спектров. Однако при этом вносятся новые ошибки, так как чем меньше граничная частота фильтра, осуществляющего предварительную фильтрацию, тем большая часть спектра самого сигнала отбрасывается. Мы видим, таким образом, что в системах сбора данных не следует применять предварительную фильтрацию, с целью устранения эффектов, относящихся к взятию выборок; назначением предварительной фильтрации должно быть только подавление (всегда присутствующих) высокочастотных компонентов шума и искажений в спектре сигнала, тогда как выборки надлежит брать с правильно выбранной частотой. На рис. 4.25 показано, что если оставить эти нежелательные составляющие, то они будут зеркально свернуты и проявятся в высокочастотной части спектра сигнала. По этой причине почти всегда входная цепь системы сбора данных содержит фильтр нижних частот. В самом конце цепочки преобразований сигнала в системе сбора данных помещают другой фильтр. Это – восстанавливающий фильтр, осуществляющий интерполяцию выходного сигнала ЦАП между моментами времени, к которым относятся выборки. В следующем разделе мы рассмотрим процедуру восстановления.

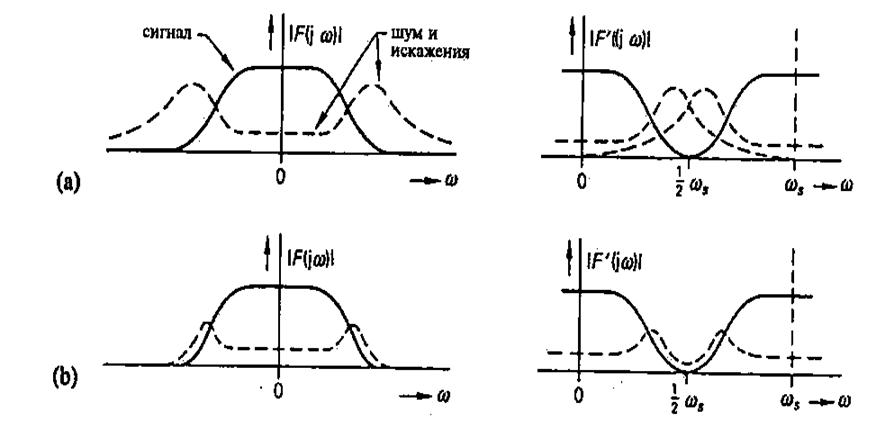
Рис. 4.25. (а) Спектр сигнала  с шумом и искажениями и соответствующий ему спектр сигнала, представленного посредством выборок. (Ь) Спектр входного сигнала после фильтрации, «предшествующей взятию выборок», и соответствующий ему спектр сигнала, представленного посредством выборок.

                                        4.5.5 Теория восстановления

   В предыдущих разделах мы увидели, что в результате взятия выборок из аналогового сигнала мы получаем дискретный по времени сигнал. Это необходимо делать, поскольку процессор способен воспринимать и выдавать информацию только в дискретные моменты времени; в системе сбора данных со стороны входа должно находиться устройство взятия выборок. На выходе системы сбора данных этот дискретный по времени сигнал необходимо снова преобразовать в непрерывный по времени сигнал, чтобы выходной сигнал был аналоговым. Это преобразование выполняется «восстанавливающим» или «интерполирующим» фильтром. Во временной области взятие выборок делает аналоговый (или непрерывный по времени) сигнал дискретным по времени, тогда как в результате восстановления этот дискретный по времени сигнал снова становится непрерывным по времени. В частотной области в результате взятия выборок возникают многократные (вторичные) копии спектра входного сигнала, тогда как в результате восстановления эти высокочастотные копии устраняются, и остается только исходный (первичный) спектр. Поскольку наше внимание сосредоточено здесь на ошибках и погрешностях в системе сбора данных (на том, как их избежать), удобно не принимать во внимание полезную работу, которую выполняет процессор с цифровым сигналом. Поэтому мы предположим, что коэффициент передачи цифрового процессора равен единице; другими словами, мы сделаем вид, что в системе сбора данных процессора нет. Тогда мы придем к модели системы сбора данных, представленной на рис. 4.26.