В соответствии со степенью точности и номинальным размерам вала-шестерни и червячного колеса принимаем соответствующие числовые значения отклонения соосности 0.016 и 0,025. [1] табл. 2.40.
Сопряжение тихоходного вала 9 с зубчатым полумуфтой 17. По параметрам рабочих поверхностей шкивов ременных передач подбираем шероховатости равные для вала Ra=0.23 мкм , для шкива Ra=0.4 мкм.[1] табл. 2.68.
Для сопряжения между тихоходного вала с зубчатым полумуфтой принимаем отклонение формы поверхностей от цилиндричности, допуск цилиндричности для отверстия 0.006, для вала 0.004. [2] табл. 2.18.
В соответствии со степенью точности и номинальным размерам тихоходного вала и зубчатого полумуфты принимаем соответствующие числовые значения отклонения соосности 0.012 и 0,020. [2] табл. 2.40.
3 Расчет посадок с натягом
3.1 Расчет и выбор посадок с натягом
Посадки с натягом предназначены для неподвижных неразъемных соединений деталей без дополнительного крепления винтами, гайками, шпонками, штифтами и т.д. Относительная неподвижность деталей при этом достигается за счет напряжений, возникающих в материале сопрягаемых деталей вследствие действия деформаций их контактных поверхностей.
В
соответствии с заданием [3] таблица П.3.1., выберем и рассчитаем посадку с
натягом d6, сопряжение червячного колеса (1) с валом-шестерней
промежуточным (2). Из таблицы [3] П.3.2., примем для данной посадки ![]() мм,
также T=40 Нм,
мм,
также T=40 Нм,
![]() кН.
кН.
Принимаем
материал сопрягаемых деталей – Сталь 60 с ![]() МПа,
шероховатость поверхности вала
МПа,
шероховатость поверхности вала![]() мкм, а отверстия –
мкм, а отверстия –![]() мкм. Значения шероховатостей
деталей принимаем по [1] таблица 2.68. Сборку осуществляем под прессом.
мкм. Значения шероховатостей
деталей принимаем по [1] таблица 2.68. Сборку осуществляем под прессом.
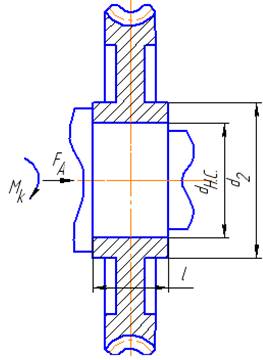
Рисунок 3.1. Схема сопряжения с натягом.
Определяем незаданные геометрические параметры деталей сопряжений
[3] c. 11:
d2= (1,6-1,8) dн.с=1,7·0,050=0,085 м; (3.1)
l =(1,4-1,6) dн.с=1,5·0,050=0,075 м;
где: ![]() –
наружный диаметр зубчатого колеса;
–
наружный диаметр зубчатого колеса;
dн.с – номинальный диаметр зубчатого колеса;
![]() –
ширина зубчатого колеса;
–
ширина зубчатого колеса;
Находим величину минимального удельного давления, возникающего на контактируемых поверхностях и необходимого для передачи крутящего момента. [1] формула 1,109:

где: f – коэффициент трения, выбираемый из таблицы [1] 1.104.
Принимаем f=0.1, поскольку обе сопрягаемые детали изготовлены из стали, [1] таблица 1.104.
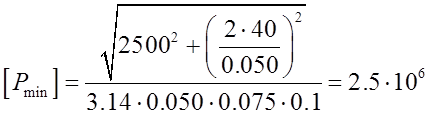 Па
Па
Рассчитываем величину минимально необходимого натяга, обеспечивающего неподвижность соединения, используя известное соотношение для определения напряжений и упругих перемещений в толстостенных цилиндрах, [1] формула 1.110:
![]() (3.3)
(3.3)
где ![]() и
и
![]() –
модули упругости материалов ступицы и вала,
–
модули упругости материалов ступицы и вала,![]() и
и
![]() –
коэффициенты Лямэ, определяемые по формулам, [1] с 334:
–
коэффициенты Лямэ, определяемые по формулам, [1] с 334:
![]() (3.4)
(3.4)
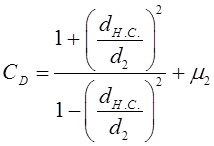 (3.5)
(3.5)
где: ![]() и
и ![]() –
коэффициенты Пуассона для ступицы и вала.
–
коэффициенты Пуассона для ступицы и вала.
Значения ![]() и
и
![]() выбираем
по [1] таблица 1.06.
выбираем
по [1] таблица 1.06.
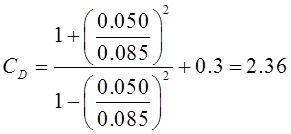 ;
;
![]() .
.
Принимаем
![]() и
и
![]() .
Из [1] таблица 1.106.
.
Из [1] таблица 1.106.
Получив все необходимые значения, подсчитаем величину минимального натяга, [1] формула 1.110:
![]()
![]() мкм
(3.6)
мкм
(3.6)
Определяем наименьший допустимый натяг с учетом уменьшения действительного натяга за счет смятия неровностей при запрессовке:
![]() (4.7)
(4.7)
![]() ,
мкм
,
мкм
Рассчитываем
максимально допустимое удельное давление ![]() ,при
котором отсутствует пластическая деформация на контактных поверхностях деталей
по [1] формулам 1.115 и 1.116.
,при
котором отсутствует пластическая деформация на контактных поверхностях деталей
по [1] формулам 1.115 и 1.116.
Для вала
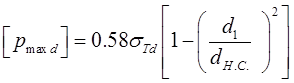 ,
МПа (3.8)
,
МПа (3.8)
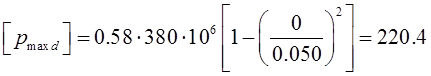 ,
Мпа
,
Мпа
Для
втулки: 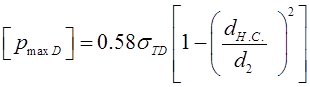 ,
МПа (3.9)
,
МПа (3.9)
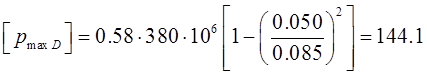 ,
МПа
,
МПа
Находим величину наибольшего расчетного натяга, для этого возьмем минимальное значение допустимого удельного давления, [1] формула 1.117:
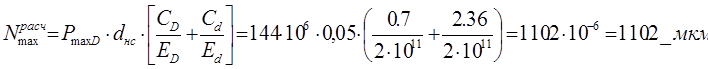 (3.10)
(3.10)
Вычисляем наибольший допустимый натяг с учетом среза и смятия неровностей, [1] формула 1.113:
![]() мкм (3.11)
мкм (3.11)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.