В соответствии с рассматриваемым методом коммутационная схема условно разбивается на левую часть, где находится блок, на вход которого поступил вызов, и правую часть, в которой находится блок с требуемым (или выбранным) для реализации данного вызова выходом. Каждый блок схемы может состоять из одного или нескольких более мелких связанных блоков. Выходы блока левой части разделены на hл направлений, равных числу блоков правой части (hл = gП), а выходы блока правой части – на hП = gЛ направлений. Левая и правая части соединяются между собой межблочными линиями. При этом выходы одного блока подключаются к входам соответствующего направления другого блока.
Работу многозвеньевой схемы можно описать, если известна взаимная доступность межблочных линий между левой и правой частями. Действительно, процесс установления соединения от заданной линии блока левой группы к выбранной линии блока правой группы коммутационной системы (рисунок 6.2) заключается в отыскании в пределах этих блоков свободной и взаимно доступной межблочной линии. Соединение будет установлено, если найдется хотя бы одна свободная и взаимно доступная межблочная линия.
Число межблочных линий, одновременно доступных слева и справа, называется взаимной доступностью
, (6.14)
где DЭ.Л и DЭ.П – эффективная доступность межблочных линий слева и справа, находятся по формуле (6.7);
Vh – число промежуточных линий между блоками.
После определения взаимной доступности коммутационная система приравнивается по пропускной способности к неполноценному пучку Vh линий, потери сообщения в котором можно рассчитать по формуле О`Делла
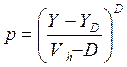, (6.15)
где Y – нагрузка, пропускаемая Vh межблочными линиями;
YD – нагрузка, пропускаемая D линиями полнодоступного пучка при потерях p. Значение YD находят по таблице Пальма или по первой формуле Эрланга (приложение А).
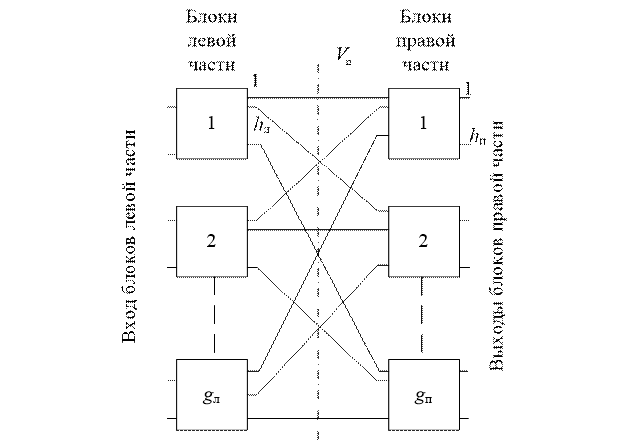Рисунок 6.2 – Процесс
установления соединения
в коммутационной системе
Формула (6.15) неявно решается относительно потерь p, потому что значением p определяется YD. Поэтому расчет потерь по формуле (6.15) осуществляется путем последовательного приближения.
Метод А. Лотце заключается в следующем. В многозвеньевых коммутационных системах потери возникают из-за отсутствия свободных выходов коммутатора первого звена, на который поступил вызов, а также из-за внутренних блокировок и отсутствия выходов последнего звена в заданном направлении. Предполагается, что указанные вероятности потерь не зависят друг от друга. При этом общая вероятность потерь в коммутационной системе
p = p0 + pk – p0pk» p0 + pk, (6.16)
где p0 – вероятность потерь из-за ограниченного количества выходов коммутатора первого звена;
pk – вероятность потерь из-за наличия внутренних блокировок и отсутствия выходов на последнем звене.
Величина p0 представляет собой потери в полнодоступном пучке из m линий, где m – число выходов коммутатора первого звена.
При большом числе входов n коммутатора первого звена и n > m величина p0 определяется по первой формуле Эрланга
p0 = EmY0, (6.17)
где Y0 – нагрузка, поступающая на m промежуточных линий между первым и вторым звеньями коммутационной системы.
В практике проектирования задаются пропущенной нагрузкой Ym. Между Y0 и Ym существует следующее соотношение:
Y0= Ym/(I – p0). (6.18)
Из этого выражения p0 определяется методов подбора.
При малом числе n вероятность поступления вызова зависит от количества обслуженных входов. При этом величину p0 определяют по формуле Энгсета
, (6.19)
где 
– число сочетаний n по m;
– пропущенная
нагрузка одним входом. Если n » m (но n > m), вероятность потерь может быть найдена по выражению
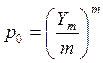. (6.20)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.