Трансмиссии и системы управления лесных машин. Выбор прототипа автомобиля. выбор и расчет двигателя, страница 14

Рассмотрим автомобиль без груза и действующие на него силы на горизонтальной плоскости (рис.7.1) и найдем статические нагрузки на оси незагруженной машины  и , для этого составим уравнения суммы моментов сил, действующих на машину относительно точек А и В:

SМ_А=0,

G_а• a - •L=0,

H.

SМ_B=0,

•L- G_а •b=0,

H.

Рассмотрим автомобиль с грузом на горизонтальной плоскости (рис.7.1) и опреде-лим нагрузки  и :

SМ_А=0,                               G_а •a- •L+•(L-)=0,

H.

SМ_В=0,                                •L-Gа•b-• =0,

 H.

Рассмотрим автомобиль с грузом при движении на руководящий подъем (рис.7.2) и определим нагрузки  и :

SМ_А= 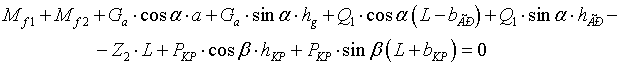             , где M_f1, M_f2 -моменты сил сопротивления качению,

,

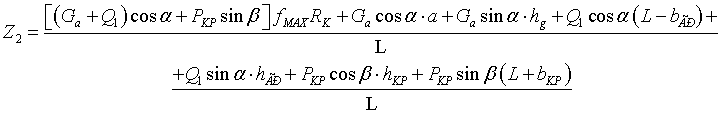
SМ_В=0,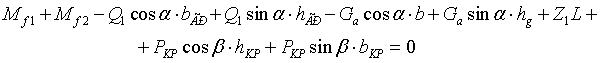          

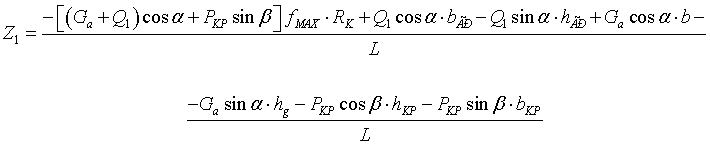
Определим числовые значения моментов сопротивления качению  M_f1, M_f2 для дви-жущегося автомобиля с грузом:

,

Н

Н,

Рассмотрим автомобиль без груза при движении на руководящий подъем (рис.7.2) и определим нагрузки  и :

SМ_А=0, ,

.

SМ_В=0

.

Определим числовые значения моментов сопротивления качению M_f1 , M_f2   для движущегося автомобиля без груза:

,

Н,

Н.

Тогда:

Произведем оценку неравномерности нагрузки на одно колесо, определив коэффи-циент неравномерности Кн и сравнив его с допустимым значением коэффициента [Кн]=1,5:

- для передних колес:

 < [Кн],

- для задних колес:

 < [Кн].

8  АНАЛИЗ УСТОЙЧИВОСТИ АВТОМОБИЛЯ

8.1 Анализ продольной устойчивости машины

Потеря продольной устойчивости наиболее вероятна при движении на подъем, когда нагрузка на переднюю ось равна нулю. Определим предельный угол продольной устойчивости a из уравнения моментов сил относительно точки В:

для незагруженной машины:

.

, для загруженной машины:

                      ,                                         (8.1)    

.

8.2 Анализ поперечной устойчивости машины

Наиболее часто потеря устойчивости автомобиля выражается в поперечном и боковом скольжении. Потеря боковой устойчивости наблюдается, как правило, при движении. 

Рассмотрим устойчивость автомобиля, движущегося на закруглении постоянного р-адиуса R=80 м со скоростью V_а на дороге с наклоном полотна b = 0º  (Рисунок 8.1).

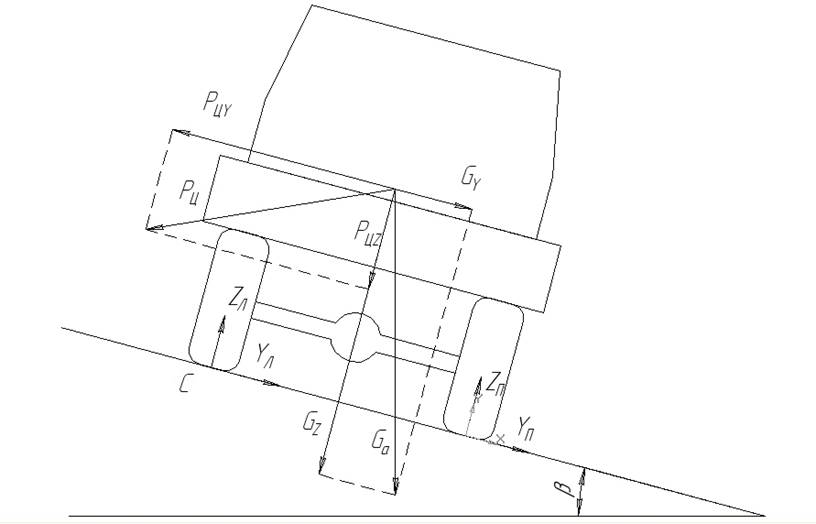
Рисунок 8.1 - Расчетная схема поперечной устойчивости автомобиля

На автомобиль действует сила тяжести G_а, которая может быть разложена на составляющие:

= G_а•cosb,

= G_a•sinb.

Составим уравнение моментов сил относительно точки С:

,

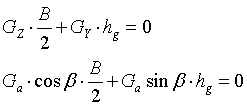Критическая скорость по условию опрокидывания:

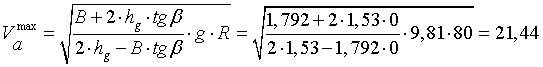м/с

Критический угол поперечного уклона по условию опрокидывания:

Критическая скорость по условию бокового заноса:

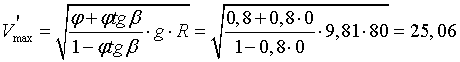м/с.

Для прямолинейного участка дороги определяем угол поперечного наклона дороги:

.

В ряде случаев возникает необходимость выяснить, что раньше происходит: опрокидывание или боковое скольжение :

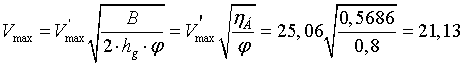м/с,

Отсюда можно сделать вывод: на дороге, где коэффициент сцепления меньше коэффи-циента боковой устойчивости (φ < h_б), первым будет наблюдаться боковое скольжение.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.  Васильев В.Н., Куликов М.И., Фрейндлинг А.Ф. Тяговые расчеты лесных машин с использованием ЭВМ. –Петрозаводск,1988.

2.  Куликов М.И., Скобцов И.Г., Перский С.Н. Тяговые расчеты лесных колесных и гусенечных машин (Часть 1). – Петрозаводск, 2007.

3.  Г.М. Анисимов и др. «Лесные машины», М. «Лесная промышленность», 1989.

4.  Г.М. Анисимов и др. «ЛЕСОТРАНСПОРТНЫЕ МАШИНЫ», М. «Экология»,1997г.

5.  П.П. Лукин и др. Конструирование и расчет автомобиля, М. 1984.