Изучение физических процессов, происходящих при взаимодействии ускоренных ионов с нанокомпозитными материалами, страница 5

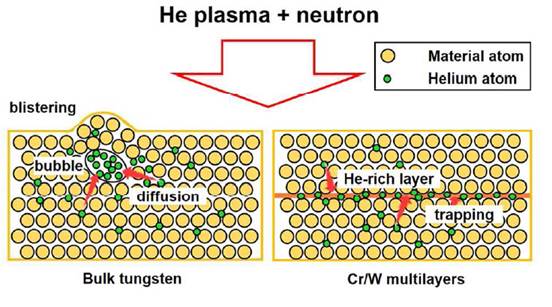
Рисунок 3. Иллюстрация эффекта захвата ионов Не на Cr/W границе, препятствующего формированию газовых пузырьков [31]

Анализ литературных данных позволяет заключить, что наноматериалы при условии оптимизации их состава и структуры демонстрируют более высокую радиационную стойкость, по сравнению с их крупнокристаллическими аналогами. Задача установления роли размерных эффектов и поверхностей раздела, выявления особенностей протекания процессов аморфизации и рекристаллизации, образования и взаимодействия дефектов, распада и взаимодействия компонентов в наноматериалах требует дальнейших теоретических и экспериментальных исследований, направленных на поиск оптимальных радиационно-стабильных наноструктур.

ГЛАВА 1. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ, ПРОИСХОДЯЩИХ ПРИ ВЗАИМОДЕЙСТВИИ УСКОРЕННЫХ ИОНОВ С НАНОКОМПОЗИТНЫМИ МАТЕРИАЛАМИ

1.1. Пробеги заряженных частиц в материалах

Пусть ион химического элемента с атомным номером Z₁, массой m₁ и энергией E₀ влетает в мишень, которая состоит из атомов химического элемента с атомным номером Z₂, массой m₂ и пороговой энергией смещения E_d. Закон сохранения энергии для данного процесса может быть записан следующим образом:

,                                               (1)

где υ(t) – скорость движения иона в материале в момент времени t на расстояниях x(t) от поверхности образца (направление движения свободного иона перпендикулярно поверхности), E(t) – потери энергии иона при его торможении на участке x(t).

Дифференцируя (1) по времени можно получить уравнение движения иона в материале:

,                                                 (2)

Удельные потери энергии иона в материале можно выразить следующей формулой:

,          (3)

где S_n – тормозное сечение, характеризующее потери энергии иона на упругие столкновения, S_e– сечение торможения, характеризующее неупругие потери энергии (взаимодействие с электронной подсистемой), N – концентрация атомов мишени, .

Из уравнения (2) с учетом (3) следует закон движения x(t):

,                                   (4)

Где , c(t-t) – функция Хевисайда.

На расстоянии L = x() имеет место остановка иона в материале. Время  определяется из условия () = 0.

,                                                        (5)

В современной радиационной физике сечения S_n, и S_e с высокой степенью точности рассчитаны для широкого диапазона энергий E₀, масс налетающих ионов и атомов мишени, значений Z₁и Z₂и других параметров процесса торможения. Учитывая статистический характер движения иона в веществе его реальным пробегом считается величина L_p, которая может быть оценена из следующего выражения [34]:

Очевидно, что в действительности около L_p имеет место статистический разброс пробегов, установить точный закон которого на сегодняшний день пока не представляется возможным. Обычно на практике в случае ионной имплантации пользуются распределениями Гаусса, Пирсон-IV и др.

Оценки пробегов ионов по формуле (6) в определенном интервале значений E₀, m₁, m₂, Z₁, Z₂дают удовлетворительное согласие с экспериментом.

При торможении иона в твердом теле идет сложный процесс передачи его энергии электронной и решеточной системам, в результате чего формируются каскады смещений атомов. «Родоначальником» каждого каскада является первично выбитый атом. Совокупность каскадов образует в свою очередь трек. Процессы же дефектообразования определяются в первую очередь значением пороговой энергии смещения атомов из узлов решетки.