Изучение физических процессов, происходящих при взаимодействии ускоренных ионов с нанокомпозитными материалами, страница 16

Рассмотрим некоторое детали процессов формирования волн деформаций при облучении твердых тел ионами и взаимодействие этих волн со структурными нарушениями решетки. Пусть Н — функция Гамильтона (точнее ее плотность) волны деформаций в кристалле, а ρ - эффективная плотность массы движущегося вещества на ее фронте. Тогда для массой скорости  волны можно записать:

,                                                    (63)

Где ,  — коэффициент, характеризующий «взаимодействие» волны с веществом и определяющий «расход» скорости при её движении по кристаллу,  ~ lΔ , l — ширина фронта ударного возмущения среды, Δ – изменение массовой скорости, обусловленное нелинейными эффектами.

Представим каскад столкновений в виде цилиндра радиуса R_Т и высотой L_c и пусть внутри нее в момент времени t = 0 генерируются прямоугольный импульс скорости ₀. Задачу рассмотрим для изотропного случая среды, используя цилиндрическую систему координат:

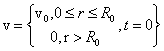,                                         (64)

Давление P₀ на границу каскада определим исходя из соотношений  и . Тогда:

  ,                                             (65)

где Е₀ — энергия налетающего иона. Решая при таких условиях уравнение (63) получим:

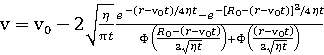,                      (66)

где Ф(х) — функция ошибок, r^’ - точка наблюдения.

Формула (66) учитывает диффузионный характер изменения скорости и в связи с этим представляет собой более общее выражение для известной в физике волновых процессов N-волны.

Давление Р во фронте волны (66) можно оценить из соотношения P = ρcv (с — скорость звука в твердом теле).

Распространяясь по кристаллу, такая волна взаимодействует с дефектами, приводя при определенных условиях к изменению их пространственного положения и термодинамического состояния. В зависимости от величины давления механизмы такого взаимодействия могут быть различными. При высоких значениях Р этот процесс идет через стадию термализации энергии упругой волны в области, искаженной дефектом. Cила взаимодействия  волны с дефектом может быть определена следующим выражением:

,                                                (67)

где Ω₀ - объем дилатации дефекта.

Если дефект характеризуется энергией активации U_m, то для его перемещения из одного равновесного положения в ближайшее другое необходима сила F_m ~ 2U_m/a₀ (а₀ - период решетки).

Динамику движения дефекта можно оценить также в рамках модели фононного газа. Действительно, силу , действующую на дефект при рассеянии фононов, можно определить из формулы:

                                =  S ,                                                (68)

где  – давление фононного газа;  – средняя концентрация фононов;  – средняя энергия фонона.

Скорость распространения фонона может быть оценена из формулы 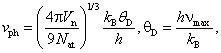где V_n – объем наночастицы; N_at – число атомов в наночастице; k_B – постоянная Больцмана; θ_D – температура Дебая; h – постоянная Планка; ν_max – максимальная частота колебаний атомов. Величина v_ph имеет порядок 10³ м/с.

Энергия колебаний E_к в кристаллической решетке по модели Дебая определяется из выражения

,                  (69)

где– функция Дебая.

Средняя концентрация фононного газа может быть определена как

                                                                                  (70)

С учетом (69) и (70) формула (68) переписывается следующим образом:

 ,                           (71)

В общем случае перемещение дефекта (например, междоузельного атома) может быть оценено из динамического уравнения:

 ,                                            (72)

где m — масса (в общем случае эффективная) междоузельного атома.

На рис. 24 (а, б) представлены результаты компьютерного моделирования процесса перемещения дефекта под действием силы F.

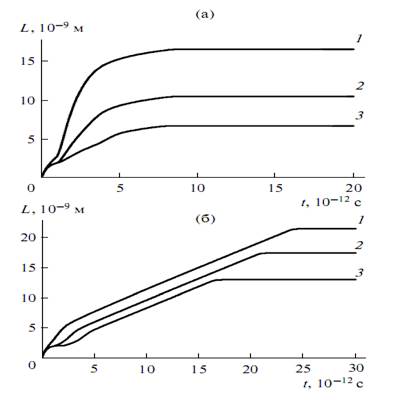
Рисунок 26. Результаты моделирования перемещения дефекта, расположенного относительно центра пика на расстояниях 8 (1), 16 (2), 24 (3) нм, для двух подходов: a – классической теории твердого тела; б – модели фононного газа.

Заключение