Изучение физических процессов, происходящих при взаимодействии ускоренных ионов с нанокомпозитными материалами, страница 14

,                                         (39)

где b – вектор Бюргерса,  - критическое напряжение, G – модуль сдвига, l – размер области, где

Для материала TiN на рис. 20 – 23 представлены соответствующие зависимости температуры T(r ,t), градиента температуры , термоупругих напряжений  и плотности дислокаций N_d(r ,t).

а)

б)

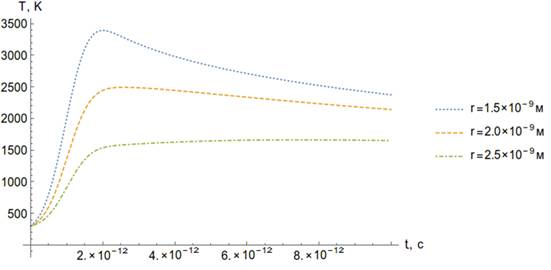
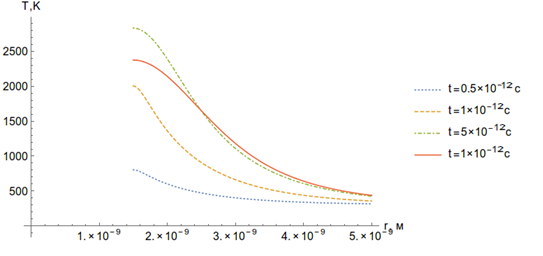
Рисунок 20. Зависимости температуры от времени (а) и пространственной координаты (б).

а)

б)

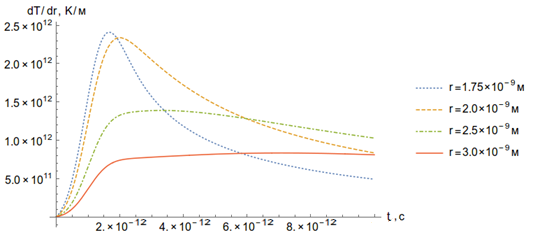
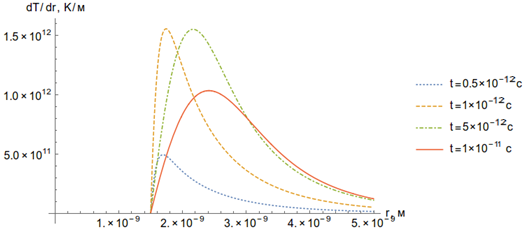
Рисунок 21. Зависимость градиента температуры то времени (а) и пространственной координаты (б).

а)

б)

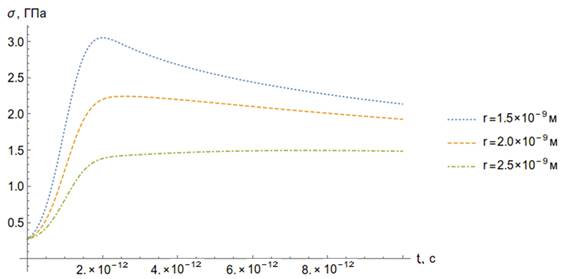
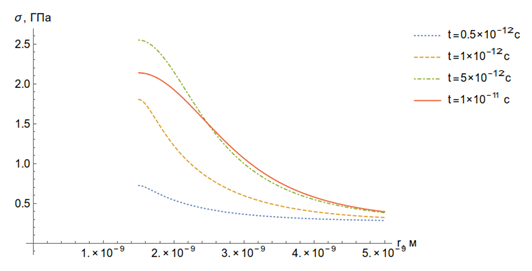
Рисунок 22. Зависимость термоупругих напряжений от времени (а) и пространственной координаты (б).

а)

б)

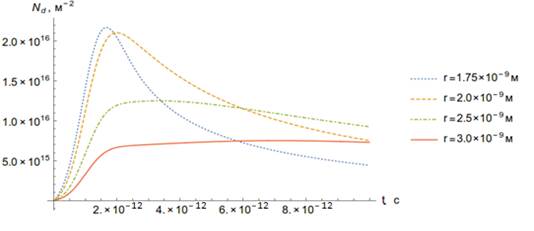
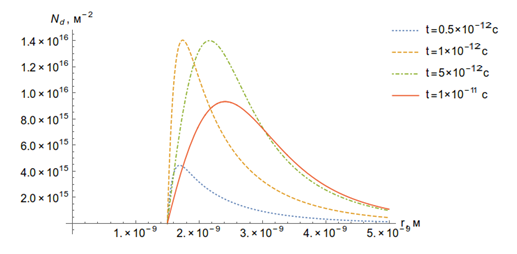
Рисунок 23. Зависимость концентрации дислокаций от времени (а) и расстояния от трека (б).

Пространственно-временную структуру температурного поля от трека иона можно определить также с помощью соответствующей функции Грина G(r ,ξ ,t-τ) . Для данной задачи функцию Грина определяем из уравнения (35) с единичным источником:

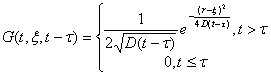,                             (40)

Тогда для температуры  решение (35) может быть записано как

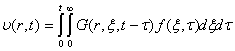,                            (41)

при начальном условии . С учетом (36) формула (41) перепишется окончательно

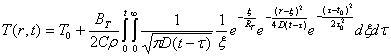,           (42)

ГЛАВА 4. ТЕРМОУПРУГОЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ НАНОСТРУКТУРИРОВАННЫХ МАТЕРИАЛОВ, ФОРМИРУЕМОЕ РАДИАЦИОННЫМ ВОЗДЕЙСТВИЕМ.

Рассмотрим термоупругие деформации в отдельной наночастице радиуса R при сферически симметричном распределении температуры T(r ,t). Уравнение равновесия в этом случае может быть записано следующим образом:

,                         (43)

где ν - коэффициент Пуассона, - вектор смещения, α - коэффициент линейного температурного расширения.

Для радиальной деформации это уравнение перепишется следующим образом:

,                                 (44)

Так как для свободной частицы напряжения σ_rr равны нулю, то

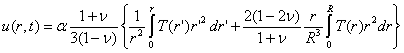,            (45)

Для данного конкретного случая используем формулу (34) для температуры T(r ,t).  Тогда можно получить:

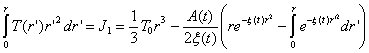,                  (46)

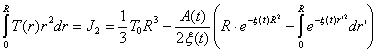 ,                 (47)

Очевидно, что относительная деформация ε(r) в произвольной точке r наночастицы определяется как du(r)/dr.

Пусть такая наночастица, характеризуемая модулем сжатия K₁, вставлена в матрицу, модуль сжатия которой K и при этом происходит рассмотренный выше разогрев включения.  Модельно это можно представить как наличие шара, вставленного в полость меньшего радиуса, вследствие чего имеет место сложный процесс деформации матрицы шаром, а шара — реакцией матрицы.  Важную роль при анализе напряженно-деформированного состояния системы будет играть максимальное температурное смещение u^(m) (R) (или соответствующая деформация ε⁽ⁿ⁾(R)) свободной наночастицы (см. формулу (44)).

В результате температурного расширения наночастицы на границе раздела r = R на матрицу со сторону включения будет действовать определенное равномерное давление P = - σ_rr . Из уравнения  следует явный вид поля смещений u(r,t):

,                                               (48)

где a и b определяются из граничных условий:

,

Тогда

,                               (49)

где E — модуль упругости Юнга.

Пусть K₁ = K (или E₁ = E). Тогда при разогреве наночастицы, когда смещение ее границы будет равно u_r(R), произойдет изменение объема ΔV . При этом а . Соответствующая деформация ε равна

,                                                 (50)

Величина ΔV - это та часть объема, на которое включение отличается от полости  уже в сжатом состоянии. Для того чтобы найти ΔV надо учесть «отдачу», то есть деформацию самого включения в результате реакции  матрицы.

Деформация матрицы  вследствие разогрева наночастицы  определяется методом Эшелби

,                                                   (51)

где  - деформационная матрица.

Для сферического включения в однородном изотропном материале эта матрица превращается в скалярную величину

,                                                (52)

Тогда давление со стороны наночастицы на матрицу будет равно: