Изучение физических процессов, происходящих при взаимодействии ускоренных ионов с нанокомпозитными материалами, страница 10

3.  Особый интерес вызывают неочевидные антикорреляционные соотношения E_d и U_b с коэффициентом температурного расширения α_T и постоянной решетки a.

В связи с этим проведем качественные оценки зависимости упругих и тепловых характеристик некоторых металлов от энергии связи, используя для простоты вычислений потенциальную энергию парного взаимодействия атомов в решетке в форме Леннард-Джонса (проблема точности здесь непринципиальна):

,

(9)

где , a₀ – равновесное значение постоянной решетки, x – смещение атома из узла решетки, вызванное механическим или температурным воздействием.

Сила реакции решетки в случае такого воздействия может быть записана следующим образом:

,

(10)

где , ,  – относительная деформация решетки, .

Для смещений x  формулу (10) можно записать как

,

(11)

где , . При этом величина A определяется следующей формулой:

,

(12)

где m_k – координационное число, a₀ – равновесное значение постоянной решетки.

Из (11) можно получить формулу для модуля упругости Юнга:

,

(13)

где .

Коэффициент температурного линейного расширения α_T оценивается по следующей формуле:

,                                                    (14)

где  – среднее смещение узла кристаллической решетки при ее нагревании, T – температура. В свою очередь:

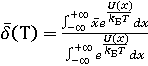,                                           (15)

где , k_B – постоянная Больцмана. С учетом формул (11), (14) и (15) получим:

.

(16)

Обратная пропорциональность α_T и U_b удовлетворительно описывает антикорреляционный характер поведения α_T и E_d (так как значение E_d прямо пропорционально U_b).

Связь температуры Дебая с энергией связи легко получить из известной формулы:

,

(17)

где h – постоянная Планка, k_B – постоянная Больцмана, v_l и v_t – продольная и поперечная скорости распространения упругих волн в твердом теле. С учетом формулы (13) получим:

,                                               (18)

Из эмпирической формулы Линдеманна (, где A – постоянная величина, V и M – молярные объем и масса вещества) и выражения (18) следует  что, в общем-то, очевидно.

Температура плавления, коэффициент всестороннего сжатия, постоянная решетки и постоянная Грюнайзена γ связаны между собой соотношением:

.

(19)

Отсюда можно получить:

,

(20)

и, как следствие:

,                                                     (21)

Такая же зависимость следует из формулы (13), если положить . Обратная пропорциональность между U_b и  получается также исходя из формулы для энергии металлического кристалла, полученной в рамках теории псевдопотенциала.

Так как пороговая энергия смещения коррелирует с U_b, то из вышеприведенных рассуждений (формулы (13), (16), (18), (20), (21)) следует удовлетворительная интерпретация представленных на рисунках 5 – 10 графиков.

ГЛАВА 2. РАЗМЕРНЫЕ ЭФФЕКТЫ В НАНОЧАСТИЦАХ

2.1. Размерная зависимость упругих свойств наночастиц

Научно-технический прогресс предъявляет все более высокие требования к материалам, используемым в различных областях человеческой деятельности. Зачастую этим требованиям традиционные вещества принципиально не удовлетворяют. В частности, это касается работы устройств и механизмов в экстремальных условиях (ТВЭЛы и материалы стенок ядерных реакторов, конструкции космических аппаратов, элементы реактивных двигателей и т.д.). Актуальной проблемой является также защита различных объектов от разрушающего действия ионизирующих излучений.