Изучение физических процессов, происходящих при взаимодействии ускоренных ионов с нанокомпозитными материалами, страница 15

,                                              (53)

где  - максимальная дилатация свободной наночастицы в результате разогрева.

Если упругие модули наночастицы и матрицы различаются, то из требования сохранения непрерывности смещений и напряжений на поверхности включения, а также равенства самих напряжений

,                                     (54)

можно получить связь между и .

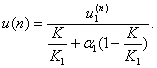 ,                                             (55)

Тогда формула для давления в матрице, обусловленного разогревом наночастицы будет иметь следующий вид

P = Ф(t)F(r,t),                                               (56)

где

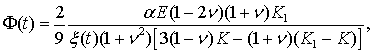                (57)

 ,  (58)

Следует отметить, что разогрев матрицы будет приводить к дополнительном возрастанию P. На рисунках 24, 25 представлены соответствующие зависимости P(r,t).

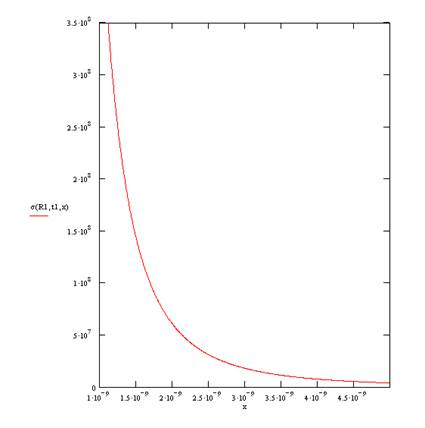
Рисунок 24. Пространственный профиль упругих напряжений в окрестности наночастицы. размером 1 нм.

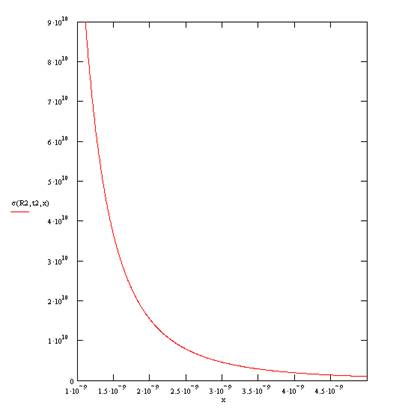
Рисунок 25. Пространственный профиль упругих напряжений в окрестности наночастицы. размером 5 нм.

ГЛАВА 5. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ФОРМИРОВАНИЯ И ЭВОЛЮЦИИ ДЕФЕКТНО-ПРИМЕСНОЙ СИСТЕМЫ В НАНОЧАСТИЦАХ ПРИ РАДИАЦИОННОМ ВОЗДЕЙСТВИИ

Экспериментально установлено, что развитие отдельного каскада смещений и всего трека в целом сопровождается генерацией упругих возмущений среды, аналогичных слабым ударным волнам. Взаимодействуя с нарушениями структуры (примеси, точечные дефекты и их комплексы), такие волны при определенных условиях могут приводить к изменению их пространственного положения и термодинамического состояния. Сила F, приводящая к таким изменениям, определяется произведением давления P во фронте волны на сечение взаимодействия волны S с дефектом. Вычисление S является весьма сложной задачей, в связи с чем имеющиеся на сегодняшний день соответствующие аналитические выражения [68] практически не применимы к конкретным расчетам.

Выражение для S получено в работе [69]:

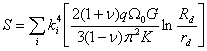,                                  (59)

Физический механизм передачи энергии волны дефекту весьма сложен и носит опосредованный характер. В начале процесса энергия волны выделяется в области, искаженной дефектом. То есть деформированная область является  местом трансформации упругой энергии. Получение же энергии самим дефектом происходит на второй стадии, когда ударный импульс трансформируется в тепловую форму движения атомов вещества. При этом в спектре частотных колебаний атомов в деформированной дефектом области при ее мгновенном разогреве находится составляющая, совпадающая с собственной частотой ω₀ самого дефекта (то есть имеет место резонанс).

Пусть спектральная функция теплового импульса в области деформации решетки имеет гауссовский вид с максимумом на частоте ω_max и полушириной δ . Соответствующие  расчеты показывают, что в этом случае дефекту по резонанcному механизму будет передана энергия:

,                 (60)

где m - масса атома,  - максимальная деформация в тепловом импульсе, l_d - величина перемещения дефекта.  Значение l_d можно таким образом оценить из следующей формулы:

,                                         (61)

Резонансный характер передачи энергии дефекту аналогичен передаче импульса налетающей атомной частицей в модели индивидуальных столкновений. В связи с этим энергетическую сторону процесса перемещения дефекта можно выразить следующим соотношением

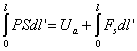,                                           (62)

где , , .

Как указывалось выше сила F, действующая на дефект, определяется давлением P и сечением S (F=P S). Остается оценить величину давления P, формируемого областью трека при торможении заряженной частицы в материале.

Касаясь эволюции пика смещений, следует отметить, что скорость нарастания давления в нем (10¹¹ ГПа/с) значительно превышает предел динамического разрушения вещества (~10⁷-10⁸ ГПа/с). Очевидно, что в этом случае следует ожидать «мгновенного» перехода ансамбля атомов в треке даже не в «расплавленное», а в «газообразное» состояние.