Изучение физических процессов, происходящих при взаимодействии ускоренных ионов с нанокомпозитными материалами, страница 13

где ω – частота волны новой фазы, M_n – спектральная амплитуда, Ω_n и Γ_n – резонансная частота и затухание, связанное с диссипацией энергии в системе, ,  ,  ,  . В рамках такого подхода переход в упорядоченное состояние представляется как процесс распространения «волны порядка» при . При этом ферромагнитная система приходит в «резонанс» при совпадении частоты воздействующей волны с собственной частотой Ω_n. Это происходит при размере наночастицы около 15 нм.

Кроме того расчет магнитной структуры наночастиц железа был проведен с помощью пакета микромагнитного моделирования Nmag с гибким методом конечных элементов с пользовательским интерфейсом на основе языка программирования Python [66]. На рис. 16-18 представлены соответствующие зависимости.

Рисунок 16. Зависимость намагниченности от размера наночастиц.

Рисунок 17. Зависимость магнитного момента то размера наночастицы.

Рисунок 18. Размерные зависимости компонентов полной магнитной энергии наночастиц.

Из полученных закономерностей следует, что магнитная структура наночастиц ферромагнитных материалов существенно зависит от их размеров.

Размерные эффекты в наночастицах имеют место также при воздействии различного рода ионизирующих излучений. Так, например, в работе [67] показано, что упругая и термоупругая реакции решетки на радиационное воздействие формируют силовые факторы, приводящие к перемещению точечных дефектов на расстояние l. Причем если , то возможен их выход на поверхность, что будет приводить в определенных случаях к уменьшению радиационных нарушений структуры.

ГЛАВА 3. АНАЛИЗ ТЕМПЕРАТУРНОГО РАЗОГРЕВА НАНОЧАСТИЦ МАТЕРИАЛА ПРИ РАДИАЦИОННОМ ВОЗДЕЙСТВИИ И ИССЛЕДОВАНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ.

3.1. Температурный разогрев радиационно-поврежденных областей наноструктурированных материалов.

Пусть при прохождении ускоренного иона с энергией Е₀  10⁴ эВ через наноструктурированный материал в наночастице выделятся энергия W₀. Тогда соответствующий температурный разогрев может быть описан следующим выражением [67]:

,                                 (33)

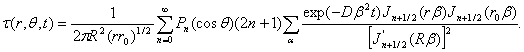
где T₀ — температура окружающей среды, C — удельная теплоемкость, ρ - плотность материала, r₀ — положение теплового источника, P_n(cosθ) - полином Лежандра, J_n+1/2(rβ) - цилиндрическая функция Бесселя полуцелого порядка, β - корни трансцендентного уравнения J_n+1/2(rβ)=0, R — радиус наночастицы, D — коэффициент диффузии тепла,

Формула (33) получена путем решения соответствующего уравнения теплопроводности методом функции Грина для несимметричной задачи параболического типа.

В предположении, что источник тепловой энергии находится в центре наночастицы (r₀=0) формулу (33) при определенных допущениях можно представить следующим образом:

,                                          (34)

где , , κ — коэффициент теплопроводности. Формулы (33) и (34) можно использовать при энергиях ионов, не превышающих 100 кэВ.

При высоких энергиях ионов (10⁵ эВ и выше), когда трек в общих чертах имеет цилиндрическую форму следует использовать общее уравнение теплопроводности с источником g(r,t):

,                                     (35)

где .

Функцию источника g(r ,t) построим в следующем виде:

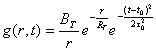, (36)

где , , 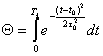R_T — радиус трека, t₀ — среднее время пролета высокоэнергетических электронов в треке, τ₀ - полуширина гауссовского распределения плотности энергии в треке (t₀~ τ₀~5·10^-15 c), T_k — время температурной релаксации процесса. Вид функции g(r,t) представлен на рис. 19.

Для решения уравнения (35) используем следующие начальные и граничные условия:

 (37)

где R_max – внешняя граница рассматриваемой цилиндрической области, H – коэффициент теплообмена.

Термоупругие  напряжения в материале определим по формуле:

, (38)

где α - коэффициент линейного температурного расширения, K - модуль всестороннего сжатия.

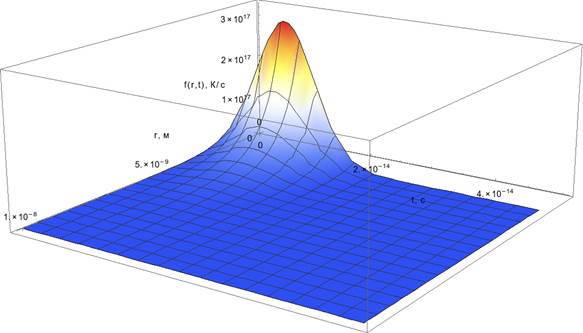
Рисунок 19. Пространственно-временная конфигурация теплового источника.

При определенных условиях разогрева будет иметь место генерация дислокаций, концентрацию которых можно определить из следующего выражения: