Изучение физических процессов, происходящих при взаимодействии ускоренных ионов с нанокомпозитными материалами, страница 11

Одним из путей повышения прочностных свойств, температурной и радиационной стойкости материалов является синтез нанокомпозитных систем, представляющих собой структурированную наноразмерными частицами матрицу. Физические свойства матрицы, отдельных наночастиц, их размеры и концентрация в совокупности определяют характеристики полученного таким образом материала. И важнейшим фактором здесь является соотношение физико-механических и теплофизических свойств отдельной наночастицы и материала матрицы с учетом архитектуры дефектности сформированной при этом приграничной области. Очевидно, что между макроскопическим и наноразмерным состояниями твердого тела должна  существовать определенная переходная зона (размерная «граница»), обусловленная изменением физических свойств материала.

Предпринимались попытки установить эту границу (l) исходя из квантово-механических принципов [50-53]. Величина l определялась путем приравнивания квантовомеханической энергии электрона (находящегося в прямоугольной потенциальной яме с учетом влияния соседних ячеек) энергии Дебая k_BT_D (k_B - постоянная Больцмана, T_D - температура Дебая). При этом получалась универсальная формула, описывающая зависимость любых физических свойств материалов от их размеров. На наш взгляд нет надобности обсуждать научную правомочность таких рассуждений. Изменение физико-механических, магнитных, теплофизических и других свойств наночастиц  может быть связано с деформацией материала, обусловленной поверхностным натяжением, уменьшением координационного числа в приповерхностном слое, изменением его группы симметрии, перестройкой архитектуры электронных оболочек, изменением энергии связи. Существенное влияние на физические свойства именно нано объектов могут оказывать также различные дефекты структуры.

Рассмотрим изменение модуля упругости Юнга Е, связанное с деформацией объема наночастицы за счет поверхностного натяжения.

Поверхностное натяжение, характеризуемое соответствующим коэффициентом s, приводит  к деформации решетки ε(r), значение которой в рамках теории упругости имеет следующий вид:

где K – модуль всестороннего сжатия объемного материала, r₀=a₀, a₀ -постоянная решетки в равновесном состоянии.

На рис. 12 приведена зависимость усредненной по объему деформации  от R.

Для качественных оценок зависимости Е(R) использовали формулу, полученную в работе [54]:

где  N - концентрация атомов решетки, U_b – энергия связи, m_k - координационное число, .

Энергию связи для простых металлов определяли из формулы для полной энергии кристалла

где  ,  ,  ,  ,  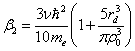,  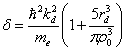,  ,  r_i -ионный радиус, r_d - радиус d-состояний, α₀ = 1.79, ν - валентность, ε₀ - электрическая постоянная, m_e - масса электрона, ρ₀ - атомный радиус.

Качественную зависимость среднего значения координационного числа от радиуса наночастицы можно представить следующим образом:

где κ=10⁸ m^-1,    - координационное число объемного материала.

Формула (25) есть результат аппроксимации соответствующих зависимостей, полученных в компьютерном эксперименте.

Относительно зависимости плотности поверхностной энергии s от размера наночастицы R имеются весьма противоречивые мнения. Так в работе [55] показано, что при уменьшении R величина s существенно возрастает. В исследованиях же авторов статьи [56] приводится аналитическое выражение для s:

где σ_V – значение s  для макрообъектов, , r_m - кратчайшее расстояние между атомами.

Формула (26) свидетельствует о противоположном характере зависимости s(R), т.е с уменьшением R величина s также уменьшается. В связи с этим в наших расчетах  значение s бралось постоянным. На рис. 13 приведена зависимость энергии связи от размеров алюминиевой наночастицы, а на рис.14 аналогичная зависимость модуля упругости Юнга для железа.