Промышленность \ Теория автоматизированного управления

Построение и преобразование структурных схем, описывающих систему управления. Дифференциальные и алгебраические уравнения, страница 14

- вектор-столбец.

2. Показатели надёжности. Мы будем рассматривать те показатели надёжности, которые отвечают за выполнение системой, предписанной ей целевой функции.

В.Б.Р. – вероятность безотказной работы. Обозначается:

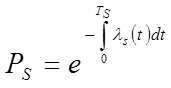
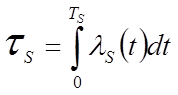- интенсивность отказа схемы конструктивной реализации.

- вероятный отказ схемы конструктивной реализации.

3. Обобщённые показатели качества. К ним мы отнесём все прочие показатели качества (масса, габариты, стоимость)

Все три группы показателей взаимно противоречивы и практически независимы друг от друга.

Для повышения надёжности наиболее эффективным является включение резервных каналов управления. В том случае, если конструктивно основной и резервный каналы совпадают, то такой резервный канал называется дублирующим и должен рассматриваться как предельный случай резервного. Включение резервного канала повышает надёжность при сохранении качества функционирования, но вступает в противоречие с обобщёнными показателями, то есть возрастают масса, габариты, стоимость.

Вернёмся к первым двум группам показателей. Введём для группы показателей функционирования следующее обозначение:

- вероятный отказ функционирования.

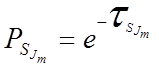
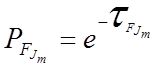
Эта операция называется строгое согласование вероятностных мер взаимнопротиворечивых случайных оценок (событий). Это выражение будем называть вероятностью безотказного (безопасного) управления или безотказность (безопасность) управления. В безопасном управлении присутствует , в безопасном - .

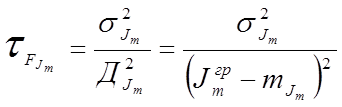- для безотказности управления.

- для безопасности управления.

Таким образом для оценки показателей функционирования надо знать три их значения:

1. - заданное. Может быть:

a) - граничное;

b) - предельное.

2. - математическое ожидание.

3. - дисперсия.

Для того, чтобы из уравнения математической модели ДСУ

, x(t₀)=x₀

получить и необходимо проинтегрировать, решить его относительно математического ожидания и дисперсии и выбрать из решения те значения переменных, которые относятся к показателям J_m. Осуществляется операция выбора с помощью матрицы наблюдателя C уравнения Y=CX.

Отсюда вывод: для этого нам необходимо осуществить операцию осреднения этой математической модели. Эта задача распадается на две:

1. решение уравнения свободного движения

Dx=A(m)x, x(t₀)=x₀

Хотя бы одна координата x₀ 0.

Осреднение простейшего ДУ.

Dx=mx, x(t₀)=1

x – переменная, m - случайная величина.

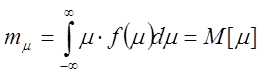
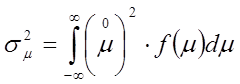
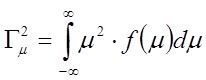-второй начальный момент случайной величины m.

Форма решения этого ДУ:

- постоянная величина.

Подставим

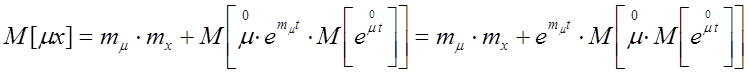Для того чтобы развернуть осреднение, надо найти .

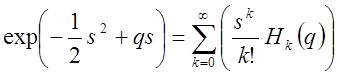- производная экспоненциальная функция.

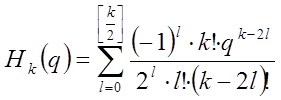- ряд Чебышева-Эрмита.

- целая часть от полученного числа.

Пусть: ,

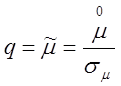
- среднеквадратичное отклонение.

Умножив правую и левую части на 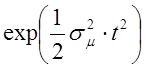, получим:

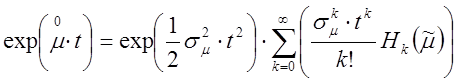
23.04.99

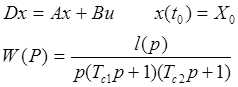
Р в первой степени говорит о том, что система имеет астатизм первого порядка, что означает, что: , - статическая ошибка, а - скоростная оценка.

Статическая ошибка определяется при постоянном входном воздействии.

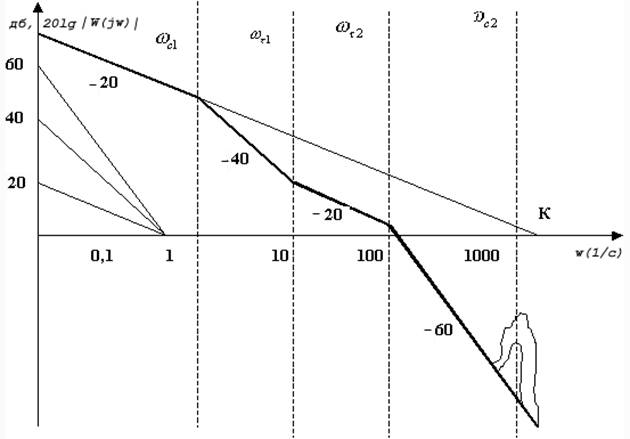
Рис. 1

В поле допуска все параметры имеют свойство случайности:

μ – вектор случайных параметров

N зависит от степени приближения математической модели к реальности.

Цель: можно ли с помощью стационарного (коэффициенты не зависят от времени) стахостического уравнения решить задачу оценки качества функционирования нашей системы.

Качество функционирования зависит от двух видов случайности:

1) Случайные параметры оператора движения (свободного) А(μ).

2) Возможные случайные составляющие u: ,