чтобы
освободиться от мнимых частей в числителе и знаменателе, домножим и числитель и
знаменатель на ![]() ,
получим:
,
получим:
![]()
![]()
![]()
Показатель колебательности для неколебательной системы М=0. У такой системы нет перерегулирования и гормонических составляющих (корни только вещественные).
Частотная область и алгебраические критерии Раута-Гурвица дают возможность косвенно опредилить, устойчива система или нет. А при использовагнии ЛАХ мы по виду частотной характиристики разомкнутой системы судим не только об ёё устойчивости, но и о точности (запретная зона по точности строится, исходя из добротности по скорости и по ускорению). Самую полную информацию о движении в системе может дать только результат интегрирования дифференциальных уравнений (ДУ), описывающих эту систему.
Решим след. задачу: как от передаточной функции или частотных характеристик перейти к линейным ДУ. В общем виде линейное ДУ может быть записано так:
Dx = Ax + Bu, начальное условие x(t0)=x0
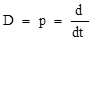 ,
,
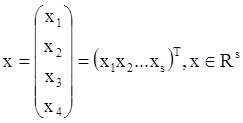 где:
где:
х – вектор столбец у которого S-координат буква Т означает транспонирование буква R- Римоново пространство (-это пространство, отвечающее ортоганальным):
R0 – точка, R1 – линия, R2 – плоскость, R3 – обьём
А-квадратная матрица размерности
S на S: 
U вектор столбец внешних
координат: ![]()
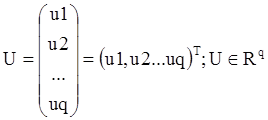
Мы рассматриваем внешние координаты двух типов:
· Управляющие (описывают управляющий сигнал)
· Возмущающие (помехи)
![]() (В – это прямоугольная матрица размерности Sxq)
(В – это прямоугольная матрица размерности Sxq)
 αд
=U1
αд
=U1
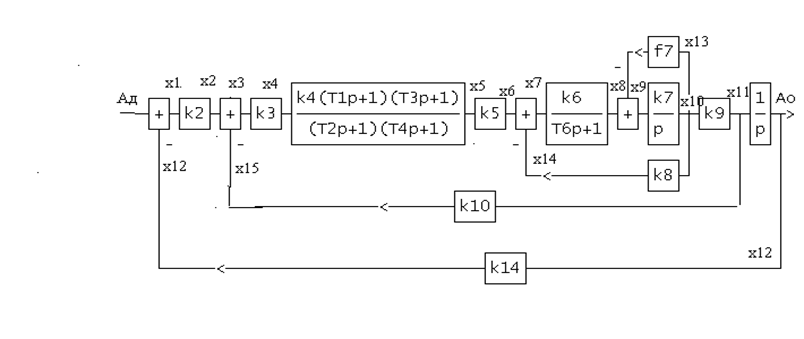
Запишем систему уравнений, соответствующих этой структурной схеме
1) x1=αд-х12
2) x2=к2-х1
3) x3=х2-15
4) x4=к3х3
5) ![]()
6) x6=к5х5
7) x7=х6-х14
8) ![]()
9) x9=х8-х13
10) ![]()
11) х11=к9х10
12) ![]()
13) х13=f7x10
14) x14=k8x9
15) x15=k10x11
Имеем 15 уравнений и 16 неизвестных U1, х1,х2,…х15
Если в первом уравнении αд =U1 задать некоторой известной функцией времени (напр. 1(t)=1 радиан, Это угол, который мы задаём на вход) то из решения системы 15-ти уравнений можно определить функции времени для всех переменных. При этом уравнения № 5, 8, 10, 12 содержат символ дифференцирования «р», а все остальные уравнения являются алгебраическими уравнениями связи (они не содержат информации о производных).
Уравнение состояния Dx = Ax + Bu содержит только дифф. уравнения и каждое из них разрешено относительно первой производной соответствующей переменной состояния. Поэтому число уравнений, входящих в уравнение состояния соответствует порядку системы S.
Из 15-ти уравнений порядок систем уравнений определяется количеством операторов дифференцирования, стоящих в знаменателе прямой цепи структурной схемы (от х1 до х12)
Порядок системы=5. Надо получить уравнение состояния 5-го порядка для этой схемы. Но прежде рассмотрим простейшие примеры.
1) ![]() рх12=х11
рх12=х11
2) ![]() Т6рх2+х8=к6х7
Т6рх2+х8=к6х7 ![]()
3)
 ,
где х41*х41=х4
,
где х41*х41=х4
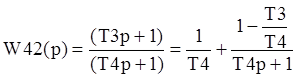
![]()
Допустим, что в уравнении №5: к4=1, Т1=Т2=Т3=Т4=0
Таким образом исключаем из системы 15-ти уравнений все переменные, кроме х8, х10 и х12. И в принятом допущении х5=х4 мы получаем уравнения:
1) ![]()
2) рх10=к7х9
3) рх12=х11
В правой части переменные х7, х9 и х11 выразятся через х8, х10, х12 и U1 через уравнение связи. Мы получим искомое уравнение состояния.
![]()
02.04.99
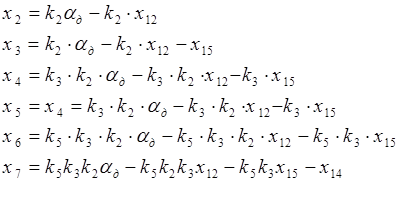
![]() X15=k10X11=k10k9X10 (подставка
уравнения 15); X14=k8k10 (подставка
уравнения14)
X15=k10X11=k10k9X10 (подставка
уравнения 15); X14=k8k10 (подставка
уравнения14)
9-е уравнение тоже, что и было и в него мы подставляем X13 из уравнения 13
![]()
разрешенные относительно 1-ой производной:

Система уравнений состояний разрешенных относительно 1-ой производной от переменных состояний, записанные в форме Каши.
![]()
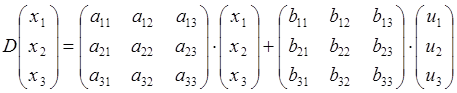 : общий вид уравнений состояний обозначим X1=X12 X2=X10 X3=X9
: общий вид уравнений состояний обозначим X1=X12 X2=X10 X3=X9
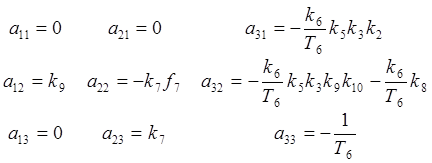
 ;
;
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.