Если пренебречь инерционными членами, устремив Jэ к нулю, то при этом исчезнут aн и bн и останутся составляющие aп и bп. Следовательно, aп и bп описывают прецессионное движение гироскопа.
Амплитуда этого движения определяется, как видно из
(19), начальными условиями. Если теперь положить 
=0, что эквивалентно исключению внешнего момента,
низкочастотное прецессионное движение исчезнет, но останется высокочастотное движение.
|
|
Таким образом, это движение является собственным движением гироскопа. Оно называется нутационным движением (или просто нутацией). Амплитуда нутации, как видно из (19), весьма мала, т.к. она обратно пропорциональна Н.
Таким образом, в разобранном случае движение гироскопа складывается из низкочастотного прецессионного (вынужденного) движения и высокочастотного движения. При этом пренебрежение инерционными членами, т.е. рассмотрение движения гироскопа в рамках прецессионной теории, эквивалентно пренебрежению нутационным движением, что в большинстве случаев вполне допустимо вследствие его малости.
Если на гироскоп действует момент, то гироскоп, как было установлено, прецессирует. Вместе с тем, согласно третьему закону Ньютона, гироскоп при прецессии должен создавать момент противодействия - момент, который равен по величине и противоположен по направлению внешнему моменту, вынуждающему гироскоп прецессировать.
Рассмотрим подробнее физическую природу упомянутого момента противодействия.
|
|
Для упрощения анализа представим себе гироскоп в виде быстро раскрученного тонкого обода. Достаточно хорошим приближением к этой модели гироскопа является велосипедное колесо, которому сообщено вращение вокруг его оси (рис.6).
Обозначим 
скорость вращения
колеса, r - радиус колеса, Jz - момент инерции колеса
относительно оси z. Допустим теперь, что колесо помимо собственного
вращения совершает вращение вокруг неподвижной оси x1, перпендикулярной z, со скоростью 
(чтобы обеспечить это вращение, необходимо,
естественно, приложить усилие к оси колеса). Рассмотрим в этих условиях
движение малого элемента колеса массой Dm, показанного на рис.6. Кроме скорости 
, обусловленной вращением колеса вокруг z,
этот элемент вращается вокруг x1 с
угловой скоростью и потому, как показывается в
курсе теоретической механики, он имеет кориолисово ускорение 
. Как нетрудно видеть, это ускорение параллельно
оси z и равно по величине
(20)
где
j определяет положение рассматриваемого элемента на
колесе, а j + p/2 есть входящий в
векторное произведение угол между векторами 
и 
. Но если элемент движется с ускорением, то
он действует на обод с силой
, равной
по величине и противоположной по направлению той силе, которая, действуя со
стороны колеса, заставляет этот элемент двигаться с ускорением .
С учетом (20)
. (21)
|
|
Эта сила имеет наибольшую величину в точках на оси x1 и наименьшую - в точках на оси y1 (рис.7); при этом на правой стороне колеса она направлена за рисунок, на левой - на нас, вследствие чего создается момент вокруг оси y1. Найдем этот момент. Плечо силы Dfz относительно оси y1 равно
и создаваемый ею момент
Определяя теперь суммарный момент, что сводится к интегрированию элементарной функции, получим
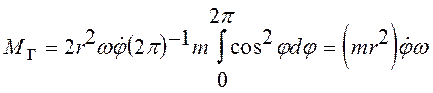
или
. (22)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
