Вища математика: Навчальний посібник (англійською мовою), страница 9

Definition. The point x₀ is called the discontinuity point of the second type if at least one of the one-sided limits at this point equals infinity.

   

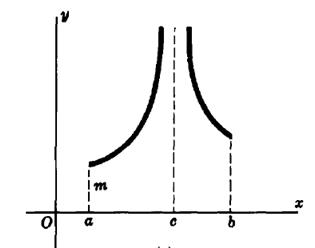
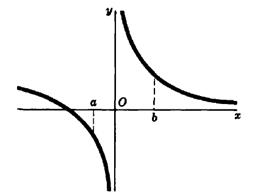
Examples.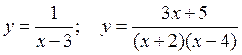

Differential calculas of the functions of one variable

Topic:The derivative of  the function of one variable

1. The  definition of the derivative of  the function of one variable.

2. Mechanical, geometrical and economic interpretation of the derivative.

3. The main rules of differentiation.

4. The table of the derivatives of the basic elementary functions.

5. Logarithmic differentiation.

6. The derivative of  the implicit function.

7. The differential of  the function.

8. L'Hopital's rule.

9. Taylor’s formula.

1.

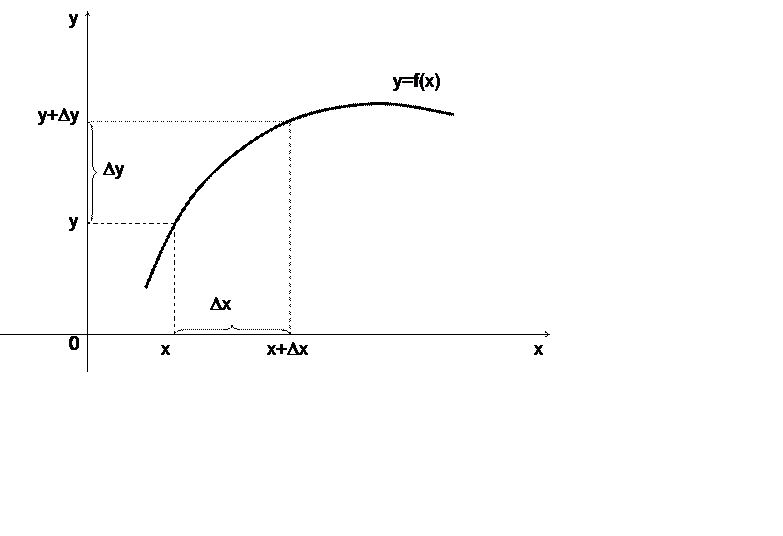
           - the increment of x

                                          - the increment of f(x)

 

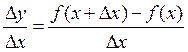- the difference quotient

 

2.1. Mechanical interpretation of the derivative:

the derivative x¢(t) is the speed of the point at the moment t, if this point moves  according the rule  x=x(t).

2.2. Geometrical interpretationof the derivative: the derivative is the slope of the tangent line to the graph of  y=f(x).

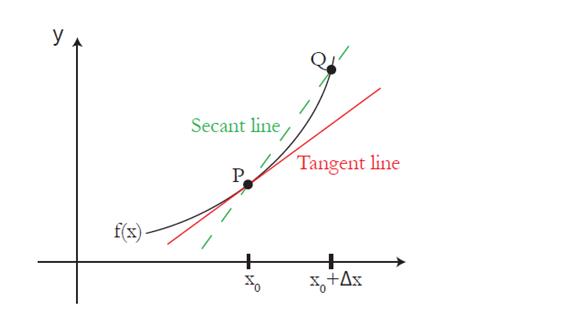
(The tangent line is called the limit position of the secant line).

2.3. Economic interpretation of the derivative:

the derivative V′(x) is the marginal cost , where  V(х) – the cost function, х – the units of production.

Topic “Function of several variables. Partial derivatives and total differentialof the function of several variables”

1.  The main definitions.

2.  Partial derivatives.

3.  Total differential.

4.  Gradient and directional derivative

We are used to deal with the function of one variable, but in practical economic activity we usually deal with the more difficult situation when one index depends on several independent factors.

Definition. If a number z is assigned (призначено) to each point (x;y) of some region D of the XY plane with respect to some rule f, then z is called the function of two independent variables. D is called the domain of definition.

Notation:  z= f (x,y).Itreadsas...

Really if we take some definite fixed values of x and y, we can calculate the correspondingvalue of z (according to the rule f).

Let’s consider some examples for finding the domain of definition of functions of two variables.

1)

The radicand should be a nonnegative value. So, to get the domain of definition of function we should find the set of all points, which coordinates satisfy the inequality: . This inequality describes a circle of radius 1 with center at the origin.

2)

Since the logarithmic function is defined only for positive numbers, the following inequality must be satisfied:  x+y>0  or  y>-x. This inequality describes the half-plane above the straight line y= - x.

In a similar manner, function of n independent variables may be defined. It’s common to introduce the notation of this function in the following way:

There is a number of differences between the functions of one and of two variables. From the other side, the calculus of functions of three or more variables differs only slightly from that of functions of two variables.

Let’s dwell on some examples.

Examples

1) As we know the area of a rectangle may be calculated according to the formula S=x·y, where x, y are sides of the rectangle.

2) Cobb-Douglas production function:

K – the capital costs,

L – the costs of the labour force,

y – the production volume,

A, α – some parameters.

3) The common form of the production function is as follows:

- the volumes of production resources.

(This function is often used in economic theory)

Geometric representation of the function of two variables:

We consider the function z=f(x,y) defined in the domain D in the plane XY (it may be an entire plane). The graph of this function is a surface in the three-dimensional space.

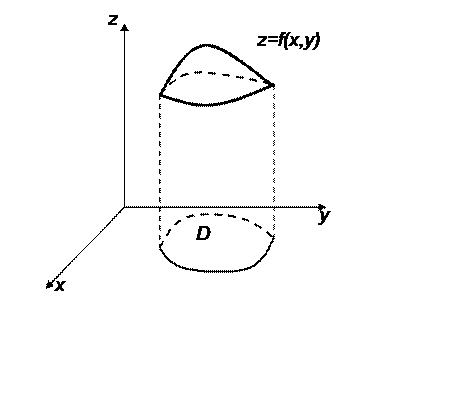
Ifinished thepresentation ofthe firstissue.

Let’s deal with the second point.

Let z=f(x,y) be a function of two independent variables x and y.