Topic. Matrices and Determinants
1.The definition of Matrix. The main notions.
2. The definitions of the Determinants of the second and third orders.
3.Properties of determinants.
4.Expansion of the determinant along the row or column.
5. Cramer’s rule.
6. The Matrix Method.
Let’s begin from the following simple economic problem (all data are in the table):
|
Type of raw material |
Consumption for unit of production |
Raw materials consumption |
||
|
№1 |
№2 |
№3 |
||
|
A |
2 |
3 |
6 |
120 |
|
B |
1 |
4 |
2 |
280 |
|
C |
7 |
5 |
3 |
240 |
1. Definition. A matrix is a rectangular array of elements. These elements are usually called entries.
Matrices are usually denoted by capital letters. For example,
 |
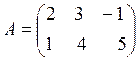 - 2x3 matrix (two by three)
- 2x3 matrix (two by three)
The common case:
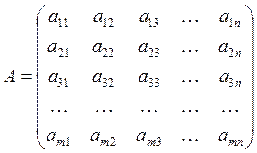 |
(you're
already familiar withthe notation of the elements with two subscripts. For instance, ![]() represents the entry at
the second row and first column of a matrix A)
represents the entry at
the second row and first column of a matrix A)
In common case the expression ![]() means
the element in the i-th row and j-th column of the matrix A.
means
the element in the i-th row and j-th column of the matrix A.
Pass to the different types of matrices:
1) A matrix with one row is called a row vector, and a matrix with one column is called a column vector.
 ;
; ![]() .
.
2) A square matrix is a matrix with the same number of rows and columns.
For example, it is the square matrix of the second order:

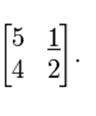 the
main diagonal
the
main diagonal
the second diagonal
3) The identity matrix In of size n is the n-by-n matrix in which all the elements on the main diagonal are equal to1 and all other elements are equal to 0.
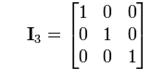
It is called identity matrix because multiplication with it leaves a matrix unchanged:
MIn = ImM = M
(for any m-by-n matrix M).
4) A square matrix A of order n is called invertible if there exists a matrix B such that
AB=BA=In.
Moreover, if B exists, it is called the inverse matrix of A, denoted A-1.
5) the transpose of a matrix A is another matrix AT created (formed) by turning the rows of A into the columns (it is the result of interchanging the rows and columns of the matrix)
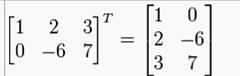
Operations onmatrices:
1) matrices of the same size can be added or subtracted element by element:
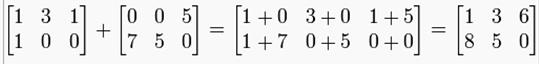
2) the scalar multiplication of a matrix A and a number c is given by multiplying every entry of A by c:

3) the rule for matrix multiplication is more complicated
Two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second.
If A is an m-by-n matrix and B is n-by-k matrix, then their matrix product AB is the m-by-k matrix whose entries are given by dot product of the corresponding row of A and the corresponding column of B:
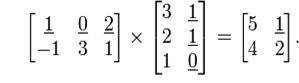
Remark. The products AB and BA need not be equal (even if both products are defined). So, the following inequality holds: AB ≠ BA.
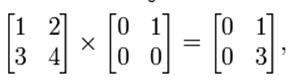
but

2. Suppose we are given the square matrix of the
second order: 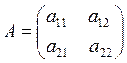 . Then we define the determinant
of A to be the scalar
. Then we define the determinant
of A to be the scalar ![]() . It is
denoted by Δ or detA or
. It is
denoted by Δ or detA or ![]() or
or  .
.
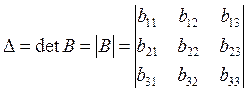 The determinant of the third-order matrix
The determinant of the third-order matrix 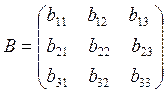 is defined by the formula:
is defined by the formula:
(it is the triangle rule)
(multiply elements located on the main diagonal, multiply elements located at the vertices of a triangle, one side of which is parallel to the main diagonal)
The scheme of the triangle rule:
3. The main propertiesof determinants
(We will illustrate the properties with a 2x2 or 3x3 examples)
1) A matrix and its transpose have equal determinants.
2) If two rows of matrix are interchanged, the determinant changes sign.
3) If two rows of a matrix are equal, the determinant is zero.
4) The common factor of the row of the determinant can be taken outside this determinant.
5) If the corresponding elements of two rows of the determinant are proportional, then the determinant is zero.
6) If a row of a matrix is zero, then the value of the determinants is zero.
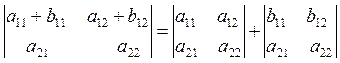 |
7)
8) If a multiple of a row is added to another row, the value of the determinant is unchanged.
Illustrate it with a 3x3 example:
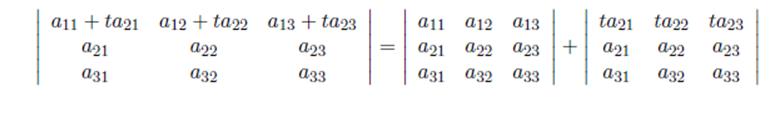
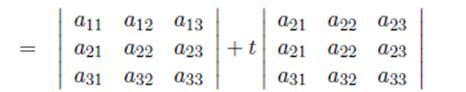

4. Let’s consider the determinant of the third order:

Let’s delete the first row and the first column of this determinant. We get the determinant of the second order, which is called the minor of the element a11. It is denoted by M11.
Similarly we can introduce the minors of the other elements.
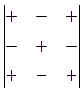 Definition.
The cofactor of the element equals the minor of this element with the corresponding sign from the chess-board pattern of signs:
Definition.
The cofactor of the element equals the minor of this element with the corresponding sign from the chess-board pattern of signs:
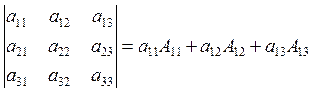 Theorem (Expansion along the row or column). The
determinant equals the sum of products of the some row elements by its
cofactors. The same holds for columns.
Theorem (Expansion along the row or column). The
determinant equals the sum of products of the some row elements by its
cofactors. The same holds for columns.
(it is the first row expansion).
5. Let’s consider the square linear system:
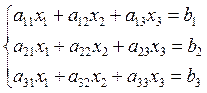 |
(1)
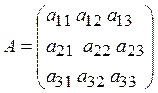 |
- the coefficient matrix
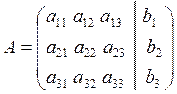 |
- the augmented matrix
 |
- the determinant of the system
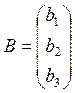 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.