Вища математика: Навчальний посібник (англійською мовою), страница 17

Topic. Applications of the definite integral

1. The geometric applications of the definite integral:

1) Plane areas by integration.

2) Length of arc.

3) Volumes of solids of revolution.

2. The economic applications of the definite integral.

1. 1) Computing of the areas of the plane figure:

 

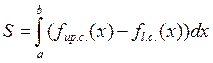This formula follows from the geometric content of the definite integral.

Examples.

 

Remark. In the tasks of these types we have to construct the graphs of the given lines. In the example 1 the first curve is a parabola. It is necessary to find the points of the intersection of the parabola with the x-axis. Really we can see that the parabola crosses the x-axis at x=0 and x=2. You often needn’t find the vertex of the parabola. To use the formula we need to know the points of intersection of two given lines. We should equate the right-hand sides of its equations, and the resulting equation will give us these points. In this example they are the limits of the integration.

 

Remark. To use the given formula we should divide the figure into two parts.

 

Remark. In the last example we should deal with the curvilinear trapezium relatively to the y-axis. In common case such trapezium has the form:

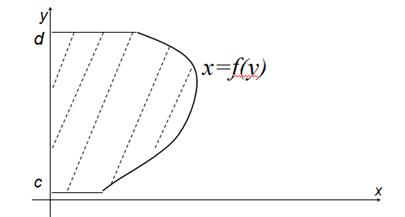
Then in this case the following formula holds:

 

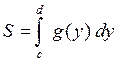1.2) Let’s assume that the given curve y=f(x) is projected on the x-axis. Let the result of the projection be the segment [a;b].

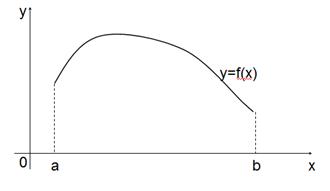
Then the length of this curve can be found by the formula:

 

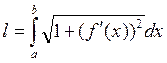Example. Find the length of the circle of radius R.

1.3) Computing of the volumes of solids of revolution

Assume that the curvilinear trapezium rotates around the x-axis. Then we will get the solid of revolution:

Then its volume can be found by the formula:

 

Example.

 

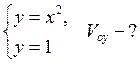Remark. To solve this task we have to deal with the curvilinear trapezium relatively to the y-axis.

There exists the generally way – with the help of the common formula:

 

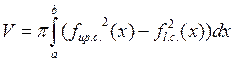The next task can be solved by this formula:

 

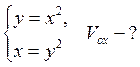2. Let’s proceed to the economic applications of the definite integral.

1) Assume that V(x) is the costs function of the manufacturing of n units of product. Then V'(x) is the marginal costs function. Therefore

 

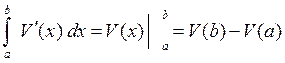Thus the definite integral of the marginal costs function equals change of the costs if the volume of production has changed.

Example. The marginal costs function has the form:

 

x – the number of production units.

Find the change of the costs if the volume of production has changed from 1000 to 3000.

2) (The mechanical content of the definite integral)

 

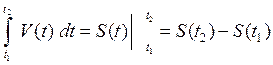Example. Find the production volume, which the worker manufactured for the second hour of his working day if the labour productivity is expressed by the function:

Topic: Improper integrals. Multiple integrals

1. Improper integral:

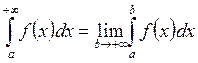We are used to consider the definite integral with the finite limits of integration. Let’s pass to consideration of another case – when one of the limits of integration is infinity. Such integrals are called the improper integrals:

If the limit equals the finite number then the improper integral is called the convergent integral, in another cases it is called the divergent integral.

Examples:

 

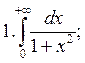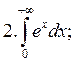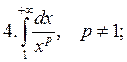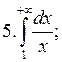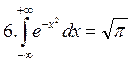Remark. The last integral is applied in the theory of probability.

2. Double integral:

 

- the double integral of the function f(x,y) over the region D.

Assume that the region D is bounded by the following lines:

 

To calculate the double integral we should pass from double integral to the iterated integral:

 

Example.

 

D: y=2x,  y=0,  x=1