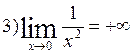Вища математика: Навчальний посібник (англійською мовою), страница 8

 

This limit means that as x becomes infinitely close to 0 then function f(x) increases infinitely.

In this case the function is called the infinitely large magnitude (at the point x=0).

 

We have to get rid of the indeterminacy: reduce the fraction and get the answer.

 

Function values vary from -1 to 1, so there is no the limit.

2. The main properties of limits

 

Let it be known that                                                          

Then the following equalities hold.

 

3. Definition. The function f(x) is called the infinitesimal magnitude or infinitesimal (at the point x₀) if                           .

Examples.

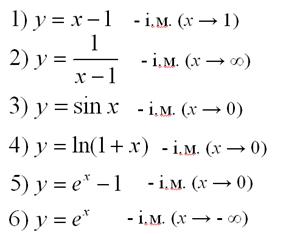
Comparisonof two infinitesimals

Let’s assume that there are two infinitesimals (at the point x₀):

 

Then

 

The result depends on the rate of approach of these functions 0. For example if α(x) approaches o more rapidly than β(x) then α(x) is called the infinitesimal of the higher order in comparison with β(x) and β(x) is called the infinitesimal of the lower order in comparison with α(x).

Definition. Two given infinitesimals (at the point x₀) are called the equivalent ones if

 

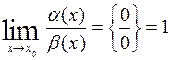Notation:     a(х) ~b(х)  (х®х₀).

The expression  is called indeterminacy. It is a symbolic expression. It means the ratio of two infinitesimals.

Examples

 

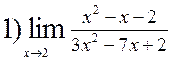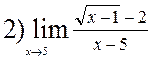(Remark for the second example. We have multiply the numerator and denominator by conjugate expression)

Consider one important rule for practice:

 

If a(х) ~b (х)  (х®х₀),then 

4. Definition. The function is called the infinitely large magnitude (at the point x₀), if

 

Examples:

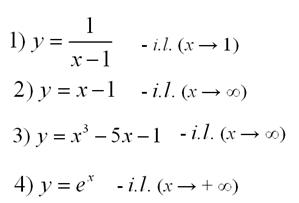
Comparisonof two infinitely large magnitudes

Let’s assume that there are two infinitely large magnitudes (at the point x₀):

 

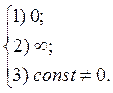
Then

Examples:

 

 

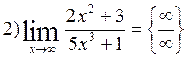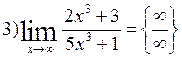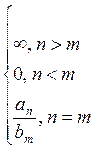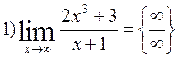Consider the common case:

 

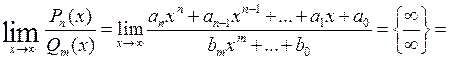Topic:Continuity of the functions of one variable

1. The main definitions.

2. The properties of the continuous functions.

3. Classification of discontinuity points.

1. Definition. A function f(x) is continuous at the point x₀ if

 

Definition. A function f(x) is continuous on some interval if it is continuous at every point of this interval

Graphically it means that the curve y=f(x) is an unbroken line.

Definition. If the function f(x) is not continuous at the point x₀ then it is said to be discontinuous at the point x_0.  In this case the point x₀ is called the discontinuity point.

2. The properties of the continuous functions

1) Any elementary function is continuous on its domain.

Example. Investigate the function    for continuity.

2) If the function f(x) is continuous on some segment [a; b] then it takes on all its intermediate values.

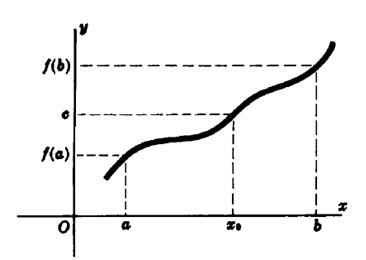
3) If the function f(x) is continuous on some segment [a; b] then it takes on its least value and its greatest value on this segment.

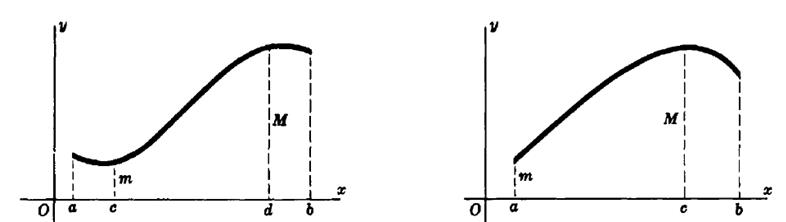
4) The function f(x) is continuous at the point x₀ if and only if

 

Remark. The limits                                            are called the one-sided limits (accordingly the limit from the left (or left-hand limit) and the limit from the right (or right-hand limit)). For example,                     means that x comes from the right, x > x₀.

Example. Investigate the given functions for continuity:

 

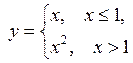3. Definition. The point x₀ is called the discontinuity point of the first type if it has the finite and different one-sided limits at this point

               

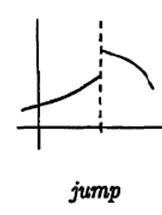
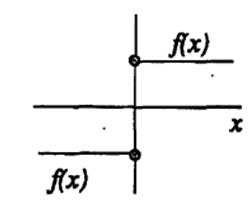
Example.