Вища математика: Навчальний посібник (англійською мовою), страница 10

Definition. If x varies while y is held fixed, then z is a function of x; its derivative with respect to x is called the partial derivative of z=f(x,y) with respect to x.

In other words we fix the variable y in assumption that x varies. So we get a function of one variable x and we can differentiate it.

Thus partial derivative of z=f(x,y) with respect to x is a limit of the difference quotient of function as the increment Δx approaches zero:

 

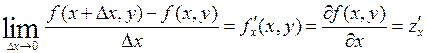Similarly the partial derivative of function with respect to y is the derivative of function with respect to y calculated on the assumption that x is a constant.

Examples. Let’s find the partial derivatives of the functions below:

 

This function is a polynomial in two variables.

When we calculate the partial derivative with respect to x we assume that only x is a variable value and y is a constant (for the period of calculation). So we have 3y as a coefficient near x² and the expression (–y⁵+1) as a constant term. Therefore the partial derivative with respect to x has the form:

 

To find the partial derivative with respect to y we assume that only y is a variable value and x is a constant:

 

Note that z’_x and z’_y are also functions of the variables x and y. The partial derivatives of them are called the partial derivatives of the second order. So there are four such derivatives:

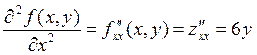- the second partial derivative with respect to x twice is obtained by differentiating twice successively with respect to x:

- the second partial derivative with respect to y twice is obtained similarly:

 

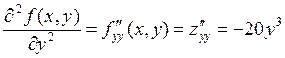- the mixed partial derivative of the second order is obtained as follows: the function is first differentiated with respect to x and then the result is differentiated with respect to y:

 

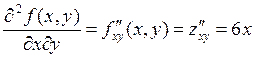Iwouldlike tomake aremark

Remark. If we first differentiate the function with respect to y and after that - with respect to x, we will obtain the same result. Really we have the following theorem:

If the function z=f(x,y) and its partial derivatives zʹ_x, zʹ_y, zʹʹ_xy, zʹʹ_yx are defined and continuous at the point M(x;y) and in some neighborhood of it then there is such equality at this point:

 

Thus the order of differentiation does notmatter. Whateverorder you use, you will find the same result.

The partial derivatives of the third order (in the general case – of the n-th order) can be obtained in the same way.

 

Find the partial derivatives of this function on your own. Keep in mind that if x is a constant then z is an exponential function and if y is a constant then z is a power function. Accordingly these facts we should use the differentiation formulas.

Let us consider the implicit function y defined by the equation F(x,y)=0. Then the derivative of function y with respect to x is calculated by the formula

.

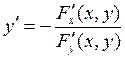Do you remember that you solved such task lastsemester but with the help of another formula? Thisway ismoregeneral and it uses the partial derivatives.

Example.

Mechanical contentsof the partial derivative

The partial derivative of function with respect to x describes the rate of change of the function in the x direction.

Economiccontentsof the partial derivative

 

1)                   - sales volume, it depends on time  t  and advertising expenses a.

 

2)                                   - production function,

       - boundary productivity with respect to resource x_i.

What do these derivatives mean?

Let’s continue. Pass to the third point.

Definition. The total differential of function of two variables z=f(x,y) is defined as expression  dz=z´_xdx+z´_ydy. It is a main part of the total increment of function and it is linear relative to dx, dy.

Example. Find the total differential of function z = 3x²y - y⁵ +1.

Since from one of the previousexamples we found that z´_x=6xy, z´_y=3x²-5y⁴, we have  dz=6xydx+(3x²-5y⁴)dy.