Вища математика: Навчальний посібник (англійською мовою), страница 14

p₂=$10,000 (10 thousand dollars) - the price of the second product,

- cost function, where x, y are the volumes of the first and second types of goods accordingly.

Find the maximum value of profit.

Example 5. Let’s consider an examplein the generalform:

Let’s set the notation:

p₀ - the market price of the product

p₁, p₂ - the market prices of the resources necessaryformanufacturingproducts

 the production function (y expresses the production volume, x₁, x₂ - the volumes of production resources)

As we know we can find the profit by the formula:

Profit:

Let’s formulate the problem: find the volumes of production resources corresponding to the maximum value of the profit

Thus wegotthe problemof testing the function of two variables for extrema:

2. Conditional extremum of function.

In many extremum problems we need to find the extremum of function of several variables which must satisfy certain equations. Let’s consider a formulation of the problem of conditional extremum in the general form:

 

In the case of this problem the function f(x,y) is called the objective function.

Thisnotationindicatesthat we should find the extremum values of the objective function inthe presence ofadditional condition.

As it was earlier we have the function of two variable, but there is also an additional requirement (or restriction) in the form of an equation (by the way, in more difficult case we could have a greater number of conditions).

Let’s consider the algorithmof finding of conditional extremum of function.

1) Construct Lagrange function. It has a form:

2) Find the stationary points from the system:

(We should find consistently all partial derivatives and after that equate them to zero. Thus we have the system from which we should get the so-called stationarypoints. We will call them suspicious of extremum)

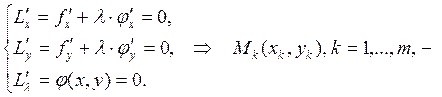 stationary points.

3) Check each stationary point for extremum (using the specific conditions of the problem).

Let’s consider some examples.

1) Assume that       the production function (y expresses the production volume, x₁, x₂ - the volumes of production resources). Let’s consider the problem: find the maximum value of the production volume if we have the cost limitation:

 

Here the each term expresses the costs of the certain resource.

(p₁, p₂ - the prices of the resources, C – the budget of the enterprise).

So we have a problem of conditional extremum:

 

Lagrange function:

 

2) In this example we will use the same notations and terminology. Let’s consider the cost function:

 

We will assume that we have the production of constant volume: 

Let’s consider the problem: find the minimum value of the cost function if we have the production of constant volume:

 

So, we came again to the problem of conditional extremum: we should minimize the function in the presence of additional conditions.

Lagrange function:

 

After that we should use the algorithm above.

3) Finally proceed to the last example:

 

This problem has a very clear geometric interpretation. Really we have the situation: the inclined(похила) planeintersectsthe cylindricalsurface (it’s as the pipeonthe roof), the result of this intersection is an ellipse. The coordinates of the highest (topmost) point and the lowest point correspond to the solution. ....

... It leads us to the solution: ...

3. We won’t solve the concrete tasks about this point and I‘d like only to tell you about this problem in general.

We shall rely on the theorem that if f is continuous on a closed bounded region D of R², then it has a global maximum (inanotherit iscalled the greatest value) and a global minimum (smallest value). We note that these must occur either at a local maximum or at a local minimum, or else on the boundary of the region D (it’s segment). Of course, in R the boundary of the region usually consists of a pair of end points, while in coordinate plane R² (it’s two - dimensional space) the situation is more complicated, because as we know the boundary of the region in R² is a curve. However, the principle remains the same. And we can test for a global maximum and a global minimum in the same way as for one variable. So we must act in accordance with the following algorithm: