Definition. Let z=f(x,y) be a function of two independent variables x and y.
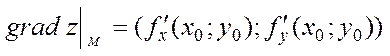 The
gradient of the function z at the point M(x0;y0)
is called a vector
The
gradient of the function z at the point M(x0;y0)
is called a vector
As we can see the coordinates of this vector are the partial derivatives of the function at the point M(x0;y0).
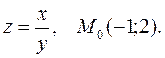 Example. Find the gradient of this function at the
point M0:
Example. Find the gradient of this function at the
point M0:
Let’s use the formula for finding the gradient. For this perform the following steps:
- find the partial derivatives of the given function,
- substitute the coordinates of the given point into these derivatives,
- write the result
I’d like to draw your attention to the important property of the gradient:
the gradient indicates the direction of function increasing with the highest rate.
- the notation of the derivative in direction of a given vector ā.
 This
derivative describes the rate of change of the
function in the direction of the vector ā.
This
derivative describes the rate of change of the
function in the direction of the vector ā.
The formula for calculating:
(it is a scalar product of these vectors; ā0 – the ort of the vector ā)
Example. Find the directional derivative of the given function at the given point:
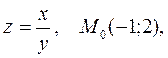 |
|||
Let’s use the formula for finding the directional derivative. For this perform the following steps:
- find the gradient (from the previous example),
- find the ort of the vector ā, for it each coordinate divide by the vector length; I remind you that we can calculate the vector length as the square root of the sum of the squared coordinates,
- calculate the scalar product of two vectors.
Topic: Investigation of function of one variable
1. Investigation of function for monotony.
2. Investigation of function for extrema.
3. Algorithm of investigation for monotony and extrema.
4. The problem of the greatest and least values of function on the segment.
5. Investigation of function for convexity, concavity and inflection points.
6. Asymptotes of a curve.
7. The general algorithm of investigation of function and construction of its graph.
1. Definition. The function is called the monotonic on the interval if it is or increasing on this interval either decreasing on this interval.
The function is said to be increasing on the interval (a; b) if y increases when the independent variable x increases:
![]() whenever
whenever ![]() in
the interval (a; b).
in
the interval (a; b).
The function is said to be decreasing on the interval (a; b) if y decreases when the independent variable x increases:
![]() whenever
whenever ![]() in
the interval (a; b).
in
the interval (a; b).
Theorem (sufficient conditions of monotony of function).
Remark. We can find the intervals of constant sign by interval method.
Example. Investigate for monotony the function y=2x3-9x2+12x.
2. Definition. The point x0 is called the point of maximum of the given function f(x), if the value f(x0) is the greatest value of f(x) on the some neighborhood of the point x0.
The point x1 is called the point of minimum of the given function f(x), if the value f(x1) is the greatest value of f(x) on the some neighborhood of the point x1.
The point of extremum is either the point of maximum or the point of minimum.

Definition. We shall say that the point x0 is a criticalpoint of the given function f(x), if it belongs to the domain of f(x) and either f’(x0)=0 or f’(x0) doesn’t exist.
Theorem (sufficient conditions of extremum of function)
If f´(x) changes its sign at the critical point x0 then x0is a point of extremum.
3. Algorithm of investigation for monotony and extrema
1) Find the domain of the function.
2) Evaluate the derivative of the function.
3) Find the critical points of the function.
4) Find the intervals of constant sign for the derivative of the function (by interval method). Set the intervals of monotony of function.
5) Check the change of sign of the derivative at the critical points of the function. Set the points of extrema.
Example. Investigate the given function for monotony and extrema:
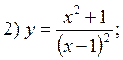 |
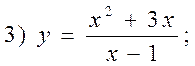 |
||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.