 |
 In this system the last two equations
involve only two unknowns. To finish we transform the second system into the
third system, where the last equation involves only one unknown. This
transformation uses the second equation to eliminate y from the third
equation.
In this system the last two equations
involve only two unknowns. To finish we transform the second system into the
third system, where the last equation involves only one unknown. This
transformation uses the second equation to eliminate y from the third
equation.
We got the so-called echelon form, which shows that z=0, substitute that back into the second equation and get y=-1, then substitute back into the first equation and get x=1. So we have the unique solution: x=1, y=-1, z=0.
I’d like to draw your attention to the advantages of Gauss method:
- it is fast and easy,
- it can be used for any linear system (independently of its size and number of solutions),
- it is safe in that it never loses solutions or picks up extraneous solutions.
We can see from the example that we used the so-called elementary operations:
- swapping,
- rescaling (multiplying by a scalar),
- pivoting (replacing by the sum of some equation and multiple of another).
As the previous example illustrates Gauss method uses the elementary operations to realize the so-called back substitution.
The theory states that the elementary operations keep the solutions. By the way the systems are called the equivalent ones if they have the coincident solutions. Thus Gauss method transforms the given system to the equivalent one which has the so-called echelon form. The solutions of that system can be found by back substitution. Consider this method with the help of the scheme :

Let’s consider some more systems.
Example 2.
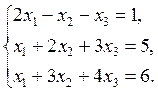 |
Here is a linear system that requires the operation of swapping equations: swap the first equation with the second one (because the second equation has the coefficient 1 of x1, it is more suitable for the further transformations, so we want to have the second equation as the pivot equation and the variable x1 as the leading one):
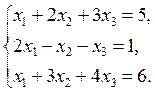 |
After this operation we can perform the next transformations (rescaling, pivoting; see the previous example). We can check on your own that the given system is a consistent determined one.
Keep in mind that there are several ways to realize Gauss method and, in particular, to get a convinient pivot equation (I mean the problem of absence of the unit first coefficient):
- we can multiply or divide the first equation by its first coefficient to get the equation with the unit first coefficient;
- we can take the another variable (for example, x2) as a leading variable;
- we can multiply the both equations by the appropriate coefficients, when we perform the operation of pivoting (to avoid the calculations with the fractions).
3. The prior systems had only one solution, but you know that there are other things that can be happen.
Let’s consider the following system.
Example 3.
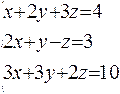 |
The first equation will be the pivot one and x will be the leading variable. So begin from the elimination x in the second and third equations. To get rid of the 2x in the second equation we multiply the both sides of the first equation by (-2), add that to the corresponding sides of the second equation and write the result in as a new second equation. To get rid of the 3x in the third equation we multiply the both sides of the first equation by (-3), add that to the corresponding sides of the third equation and write the result in as a new third equation. After these transformations we have got the following system:
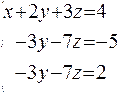 |
We can see that we got the equal (coincident)
left-hand sides of two last equations and the different right-hand sides of them). These equations are called contradictory ones. Any values of the variables can’t satisfy these equations simultaneously, so the given system is inconsistent because it hasn’t any solutions and the solution set is empty.
Let’s pass to the third case: we will see how to describe the solution set of a system of many solutions.
Example 4.
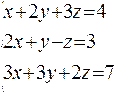 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.