Применение теории случайных процессов, страница 20

Для построения квазиоптимальных фильтров выразим среднеквадратическую ошибку через спектральные плотности мощности некоррелированных сигнала и аддитивной помехи. Структурная схема устройства, формирующего случайный процесс  из сигнала  и шума , приведена на рис. 3.4, где  – комплексная частотная характеристика квазиоптимального фильтра.

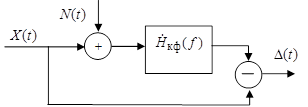
Рис. 3.4

Из данного рисунка следует, что спектральная плотность мощности процесса  равна

.

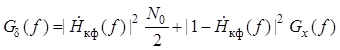В этом случае среднеквадратическая ошибка

.        

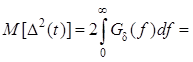
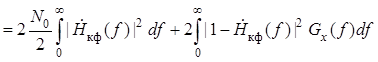Пример 3.2 (продолжение примера 3.1). Используем в качестве квазиоптимального фильтра Винера идеальный фильтр нижних частот с передаточной функцией

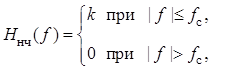                         где  – частота среза,  – коэффициент усиления. Эти два параметра подлежат определению при оптимизации данного фильтра. Подставив в , получим

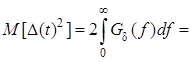
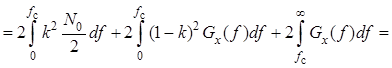
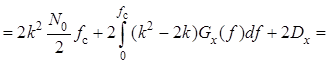
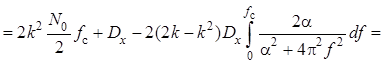
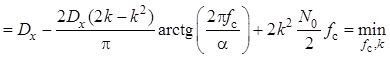, где  – спектральная плотность мощности случайного процесса . Оптимальные значения параметров квазиоптимального фильтра можно найти, приравняв к нулю частные производные этого выражения по  и . К сожалению, полученная при этом система уравнений является нелинейной и ее точное решение затруднительно. Однако, как показывает анализ, достаточную точность имеет решение, которое можно найти при линеаризации функции :

.

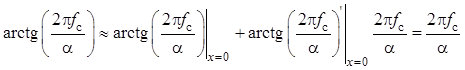В этом приближении оптимальные параметры равны

, .

3.2.3. Помехоустойчивая оценка линейно искаженных случайных сигналов

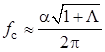В некоторых радиотехнических системах сигнал искажается не только шумом, но и линейной системой с известной импульсной характеристикой. Например, по данным измерения, скорости объекта  необходимо оценить траекторию его перемещения . Связь между  и  описывается линейным оператором (перемещение равно интегралу от скорости).

Пусть наблюдаемый процесс

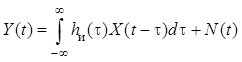, где  – импульсная характеристика искажающей линейной системы. Оцениваемый процесс  и шум  являются некоррелированными случайными процессами с известными спектральными плотностями мощности  и . Тогда, используя соотношения, приведенные во втором разделе, получим

,                     

.                             

В этом случае комплексная частотная характеристика фильтра Винера и минимальная среднеквадратическая ошибка соответственно равны

,                    

.

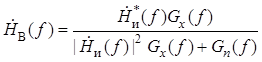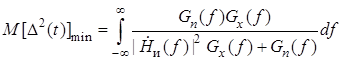При отсутствии шума () фильтр Винера вырождается в так называемый инверсный фильтр

.

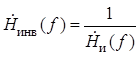Инверсный фильтр, по сути, является обратным оператором по отношению к искажающему фильтру .

Пример 3.3. Предположим, что наблюдаемый сигнал

, где дифференцируемый оцениваемый процесс  и белый шум  являются некоррелированными взаимно стационарными случайными процессами с известными спектральными плотностями мощности  и .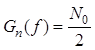

Если для оценки  использовать инверсный фильтр, который в данном случае будет идеальным интегратором, то

.

Отсюда следует, что непосредственное интегрирование наблюдаемого сигнала  приведет к тому, что дисперсия шума на выходе интегратора (см. пример 2.7), а следовательно, и среднеквадратическая ошибка оценивания будут бесконечно большими. Это объясняется тем, что при  амплитудно-частотная характеристика инверсного фильтра . Поэтому даже при малых интенсивностях белого шума дисперсия шума на выходе интегратора равна бесконечности.

Комплексная частотная характеристика дифференциатора

, тогда

,                         

.                 

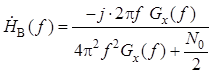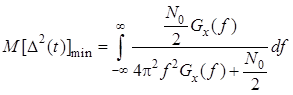Определенный интеграл в для дифференцируемого процесса  сходится, т.е. среднеквадратическая ошибка оценивания не равна бесконечности. В отличие от инверсного фильтра,  при . Это свойство амплитудно-частотной характеристики фильтра Винера обеспечивает конечность среднеквадратической ошибки оценивания.

3.3. Вопросы и задачи

1.  Почему значение константы  в не влияет на отношение сигнал/шум на выходе согласованного фильтра?

2.  Что общего между сигналом  и ковариационной функцией шума  на выходе согласованного фильтра?