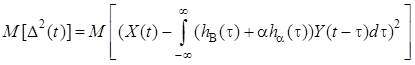Применение теории случайных процессов, страница 18

      больше, чем при . Поэтому производная от по параметру  при  равна:

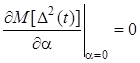,                                 или с учетом

.                     

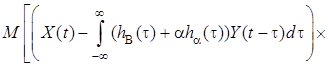
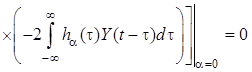Подставив в  и проведя несложные преобразования, получим

.         

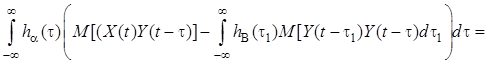
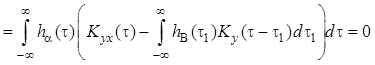Очевидно, что данное равенство будет всегда выполняться при равенстве нулю выражения в скобках, т.е. когда

.                      

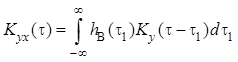Уравнение называется уравнением Винера–Хопфа. Импульсная характеристика , удовлетворяющая уравнению Винера–Хопфа, минимизирует среднеквадратическую ошибку, а фильтр с такой характеристикой называется фильтром Винера. Поэтому задача синтеза оптимального фильтра сводится к решению интегрального уравнения Винера–Хопфа относительно . Очевидно, что интеграл в представляет собой интеграл свертки. Взяв преобразование Фурье от левой и правой частей уравнения Винера–Хопфа, получим

, откуда

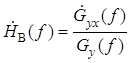,                                  где  – комплексная частотная характеристика фильтра Винера,  – взаимная спектральная плотность мощности наблюдаемого случайного процесса  и сообщения ,  – спектральная плотность мощности . Здесь учтено, что  является вещественной функцией [5]. Импульсную характеристику фильтра Винера можно найти, взяв обратное преобразование Фурье от . На этом синтез фильтра Винера завершен.

Найдем минимальное значение среднеквадратической ошибки для линейного фильтра. В общем случае

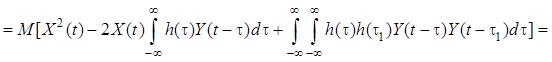
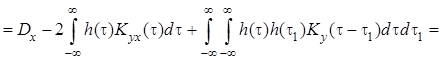
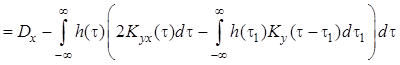,       где  – дисперсия сообщения . Из с учетом уравнения Винера–Хопфа следует, что минимальное значение среднеквадратической ошибки линейной оценки

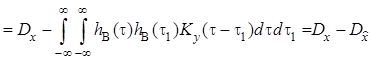,          где  – дисперсия оценки . Здесь учтено, что оценка является реакцией линейной системы с импульсной характеристикой  на случайный процесс  и, следовательно, ее дисперсия определяется формулой . Таким образом, минимальная среднеквадратическая ошибка равна разности дисперсий оцениваемого процесса и его оценки, которые можно выразить через интегралы от соответствующих спектральных плотностей мощности следующим образом

,                                 

.               

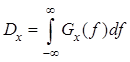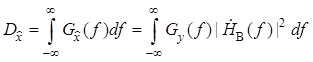Для определения была использована формула . Подставив и в , выразим величину минимальной среднеквадратической ошибки  через интеграл от разности спектральных плотностей мощности

.           

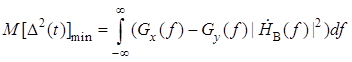Подставляя в выражение для передаточной функции фильтра Винера , получим

.               

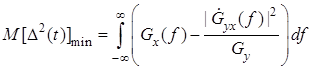Приведем выводы по полученным результатам.

1.  Из уравнения Винера–Хопфа следует, что для отыскания оптимальной линейной оценки необходимо знать только  и  (или  и ). Для вычисления минимальной среднеквадратической ошибки также необходимо знать эти характеристики. Любые другие статистические характеристики сигнала и помехи оказываются бесполезными.

2.  Для всех гауссовских и негауссовских процессов, имеющих одинаковые  и , оптимальный линейный фильтр является одинаковым и обладает одинаковой среднеквадратической ошибкой.

3.  Если сообщение , помеха  и наблюдаемый сигнал  являются совместно гауссовскими стационарно связанными случайными процессами, то фильтр Винера является абсолютно оптимальным, т.е. обеспечивает минимальную среднеквадратическую ошибку в классе всех возможных систем как линейных, так и нелинейных. Это следует из того, что для центрированных гауссовских случайных процессов ковариационные функции являются исчерпывающими характеристиками [5].

4.  Для фильтра Винера ошибка не коррелирована с наблюдаемым сигналом . Это свойство непосредственно вытекает из :

.

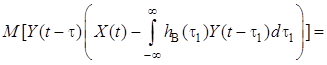
5.  Если сообщение , помеха  и наблюдаемый сигнал  являются совместно гауссовскими стационарно связанными случайными процессами, то ошибка статистически не зависит от наблюдаемого сигнала. Это свойство вытекает непосредственно из того, что некоррелированные гауссовские случайные величины являются статистически независимыми [5].

3.2.2. Фильтр винера для сигнала, не коррелированного с аддитивной помехой

Если оцениваемый процесс  и шум  являются некоррелированными случайными процессами и

, то ковариационная функция наблюдаемого процесса  и взаимная ковариационная функция  и сообщения :

,                             

.