Применение теории случайных процессов, страница 12

Критерий минимума среднеквадратической ошибки оценивания

                      применяется для выделения случайных сигналов из помех, т.е. когда необходимо получить сигнал , который как можно более точно воспроизводил бы полезный информационный сигнал . Здесь и далее  обозначает оценку процесса ,  – мгновенную ошибку оценивания.

Критерий максимума отношения сигнал/шум обычно применяется для решения задачи обнаружения или различения детерминированных сигналов. Пусть наблюдаемый сигнал

,                                 где  – детерминированный сигнал;  – аддитивный шум наблюдения. Так как фильтр является линейной системой, то с учетом принципа суперпозиции сигнал на выходе фильтра будет

, где  и  – отклики линейной системы соответственно на  и . Тогда критерий максимума отношения сигнал/шум имеет вид

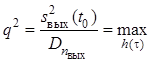,                                  где  – отношение сигнал/шум, вычисленное для момента времени ,  – дисперсия шума ,  – импульсная характеристика искомой линейной системы. Как будет показано далее, фильтр, синтезированный по этому критерию, существенно искажает форму сигнала.

3.1. Фильтр, максимизирующий отношение сигнал/шум (согласованный фильтр)

3.1.1. Постановка задачи

Сформулируем исходные данные для синтеза фильтра, максимизирующего отношение сигнал/шум .

Пусть наблюдаемый сигнал представляет собой аддитивную смесь сигнала  и шума , т.е. определяется формулой . Сигнал  полностью известен. Это означает, что заданы его форма и время прихода. Шум  является белым шумом с нулевым математическим ожиданием и ковариационной функцией

.                                   

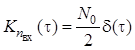Требуется синтезировать физически осуществимый линейный фильтр с постоянными параметрами, обеспечивающий на выходе в заданный момент времени  наибольшее возможное отношение квадрата пикового значения сигнала к дисперсии шума

.                                

3.1.2. Синтез согласованного фильтра

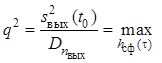Выполним синтез фильтра, т.е. найдем импульсную характеристику фильтра, удовлетворяющую критерию . Пусть входной сигнал имеет спектральную плотность

,                  где  – модуль спектральной плотности сигнала (амплитудный спектр),  – фаза спектральной плотности сигнала (фазовый спектр).

Спектральная плотность сигнала на выходе фильтра с учетом и равна:

,                  где  – комплексная частотная характеристика искомого фильтра,  и  – его амлитудно-частотная и фазо-частотная характеристики. Взяв обратное преобразование Фурье от спектральной плотности , получим сигнал  на выходе фильтра:

.       

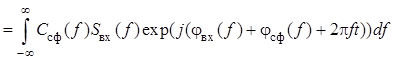В момент времени  сигнал на выходе фильтра

.      

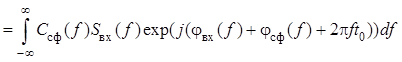При действии на вход линейного фильтра белого шума со спектральной плотностью мощности дисперсия шума на выходе фильтра с учетом

.                            

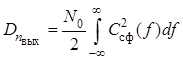Подставив и в , получим выражение для отношения сигнал/шум на выходе линейного фильтра в момент времени :

.                                        

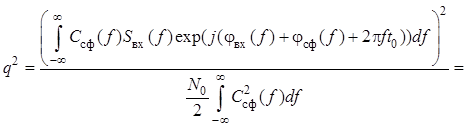
Задача определения оптимальной комплексной частотной характеристики фильтра  связана с нахождением экстремума . Для этого используем неравенство Буняковского–Шварца [8]:

.          

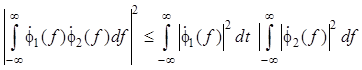Выполнив преобразование числителя в формуле с учетом , получим

.

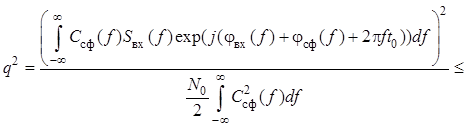
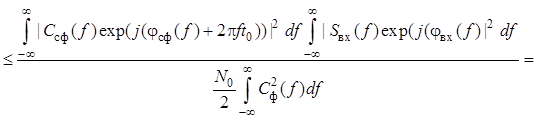
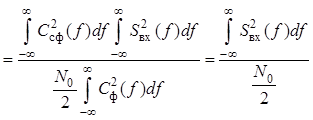Таким образом,

.                                   

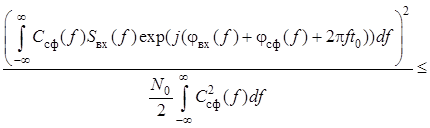
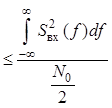Неравенство перейдет в равенство, т.е. отношение сигнал/шум  достигнет максимума при

                                  и

,                            где  – не равная нулю некоторая произвольная постоянная величина.

Таким образом, комплексная частотная характеристика оптимального фильтра, удовлетворяющего критерию , равна

.                           

Фильтр с комплексной частотной характеристикой называется согласованным, так как его амплитудно-частотная и фазочастотная характеристики согласованы с амплитудным и фазовым спектрами входного сигнала. Фазочастотная характеристика согласованного фильтра отличается от фазового спектра входного сигнала только знаком и линейной функцией частоты , а его амплитудно-частотная характеристика с точностью до константы равна амплитудному спектру входного сигнала. Сомножитель  в представляет собой комплексную частотную характеристику линии задержки сигнала на .