Применение теории случайных процессов, страница 2

.

Спектральная плотность такой функции равна единице для всех :

.

Поэтому реакция линейной системы на дельта-функцию

,        где  – обратное преобразование Фурье. Отклик линейной системы  на дельта-функцию называется импульсной характеристикой, которая в соответствии с связана преобразованием Фурье с комплексной частотной характеристикой .

В табл. 1.1. приведены импульсные и комплексные частотные характеристики для некоторых линейных систем.

Преобразование Фурье от произведения равно интегралу свертки импульсной характеристики  и входного воздействия , т.е.

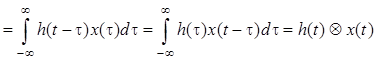,           где  – символ интеграла свертки.

Таблица 1.1

Соотношения для некоторых линейных систем

Окончание табл. 1.1

¹ Здесь входным сигналом является ток, а выходным – напряжение на контуре.

² Здесь входным сигналом является напряжение на RLC цепи,  а выходным – напряжение на емкости.

Таким образом, линейная система с постоянными параметрами характеризуется тем, что ее отклик  получается суперпозицией (сложением) всех значений входного воздействия , каждое из которых умножается на весовой коэффициент , где  – разность моментов наблюдения процессов на выходе и входе линейной системы. Зная импульсную характеристику линейной системы, можно по формуле определить выходной процесс  для произвольного входного воздействия . Например, реакция линейной системы на входной сигнал согласно выражается через комплексную частотную характеристику следующим образом:

.

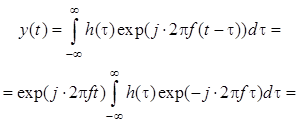
Линейная система называется каузальной, если ее импульсная характеристика равна нулю при отрицательных значениях , т.е.

.                                     

В противном случае система называется некаузальной. Для каузальных линейных систем выражение с учетом условия имеет вид

.        

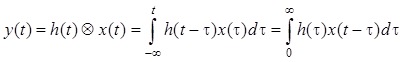Из данного соотношения следует, что у каузальных систем отклик на выходе  в момент времени  зависит от значений входного воздействия  при , т.е. отклик на выходе каузальной линейной системы не может появиться раньше входного воздействия.

Если входное воздействие  было равно нулю при , то формула примет вид:

.       

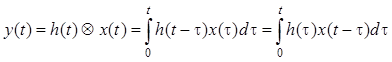Таким образом, для некаузальной линейной системы в установившемся режиме процесс на выходе линейной системы определяется соотношением . При учете каузальности интегрирование ведется только для положительных значений аргумента импульсной характеристики [формула ]. В тех случаях, когда рассматриваются переходные процессы в линейной системе, используется формула , т.е. полагается, что при  входной процесс . Комплексная частотная характеристика используется, когда интересуются лишь стационарным состоянием каузальной или некаузальной линейной системы, т.е. когда переходные процессы в системе завершились и входной и выходной процессы являются стационарными.

Стационарная линейная система является устойчивой, если произвольное, но ограниченное воздействие вызывает отклик, также являющийся ограниченным. Так как для ограниченного воздействия  существует некоторая постоянная  такая, что для всех

, то

.

.                  

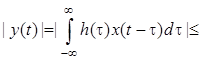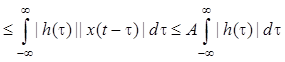Из следует, что импульсная характеристика  устойчивой стационарной линейной системы абсолютно интегрируема, т.е.

.

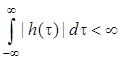Для линейных систем с постоянными параметрами комплексная частотная характеристика обладает следующими свойствами симметрии:

,

,