Конспект лекций по дисциплине "Теория вероятностей и математическая статистика", страница 4

 – тангенс угла наклона β к оси ОУ, касательной к линии пересечения поверхности  и плоскости у = у₀.

Физический смысл

 - скорость изменения функции  в направлении координатных осей.

Определение  Полным дифференциалом функции  называется главная линейная относительно  и  часть полного приращения функции .

Пример   ;    

;    ;

  dz                                     γ

dz– содержит Δх, Δу только в первой степени, это дифференциал z, γ содержит Δх, Δу в старших степенях и является б.м. величиной более высокого порядка, чем , т.е..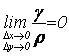

, при этом  – частный дифференциал функции z по х;   – частный дифференциал функции z по у.

По аналогии с функцией одного переменного можно находить частные производные любого порядка ; ; ;  и т.д. Для функций двух переменных в нашем курсе , т.е. порядок дифференцирования не важен.

Пример : ; ;  ;  ;  ;  ;  .

Определение  Функция  имеет max в т. M₀ (х₀, у₀) Î D – области определения , если существует окрестность т. M₀, в которой для любой т. M (х, у) выполняется неравенство .

Если  в окрестности т. M₀ (х₀, у₀), то говорим, что в т. M₀ функция  имеет min.

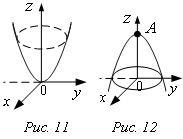Примеры : 1)  – параболоид вращения, функция в т.О(0, 0) имеет min; .

В пространстве точка min – точка О(0,0,0) (рис. 11).

2)  или – смещенный параболоид вращения (рис. 12). Функция z в т.А (0, 0, 1) имеет max.