Равновесная химическая термодинамика. Основы классической термодинамики. Термодинамическое описание химических процессов, страница 7

Переход i-го компонента из фазы  в фазу  можно рассмотривать как химическую реакцию

в равновесии:

поэтому

Аналогичные равенства химических потенциалов справедливы и для всех остальных фаз и компонентов. В итоге приходим к набору условий, которые должны выполняться при равновесии:

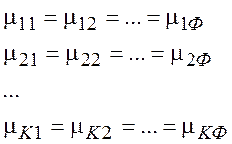                                                                                                 (6.2)

Общее число таких условий равно  (Ф - 1)K. С другой стороны, минимальное число параметров, которое нужно знать, чтобы охарактеризовать гетерогенную систему равно KФ + 2 – Ф   (КФ - полное число переменных A_ij ;  два дополнительных параметра – это полное давление и температура; Ф - число условий на концентрации в фазах, так как в любой фазе сумма мольных долей). Поэтому вариантность гетерогенной системы (число степеней свободы) равна

        (правило фаз Гиббса)                     (6.3)

Глава 7. Термодинамика смесей

7.1. Однородные функции

 Функция называется однородной порядка m относительно переменных n_i , если

                                                                   (7.1)

Для  справедливо

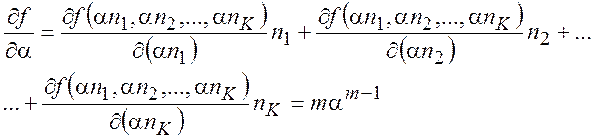                                            (7.2)

В термодинамике обычно встречаются функции первого (экстенсивные) и нулевого порядка (интенсивные).К однородным функциям первого порядка относятся G, V и др. Из уравнения (7.2) следует, что для однородных функций первого порядка можно написать, полагая

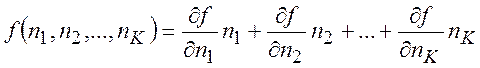                                                        (7.3)

7.2. Уравнение Гиббса-Дюгема

Уравнения Гиббса-Дюгема устанавливают связь между термодинамическими параметрами и составом смеси. Рассмотрим для некоторой фазы орднородную функцию первого порядка относительно переменных n_i :  . Это может быть G, V и др. Для  в общем случае можно написать

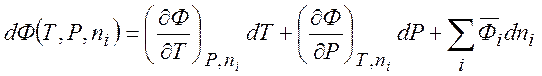                                              (7.4)

Учитывая, что функция  однородна

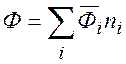
и

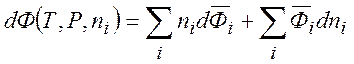                                                                             (7.5)

Получаем уравнение Гиббса-Дюгема:

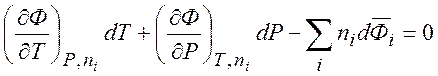                                                               (7.6)

Например, для энергии Гиббса получаем

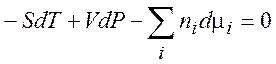                                                                                          (7.7)

Уравнение Гиббса-Дюгема справедливо во всех случаях, независимо от того, находится система в равновесии или нет. На практике в качестве параметров удобно рассматривать мольные величины и мольные доли:

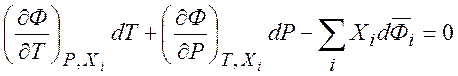                                                            (7.8)

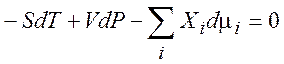                                                                                         (7.9)

7.3. Функции смешения

Функция смешения равна разности мольной величины  смеси и суммы величин , характеризующие чистые вещества, в соответствии с их мольной долей  :

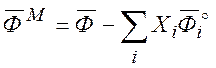                                                                                                  (7.10)

Например, функция смешения для энергии Гиббса

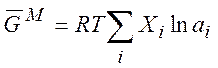                                                                                                  (7.11)

В идеальной смеси

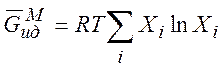                                                                                                 (7.12)

Найдем энтальпию смешения. Учитывая соотношение Гиббса-Гельмгольца

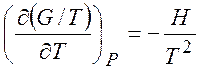
и, следовательно,

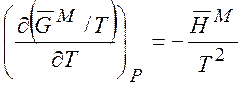
находим

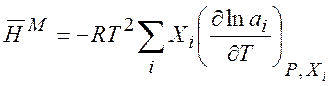                                                                              (7.13)

В идеальной смеси энтальпия смешения равна нулю:

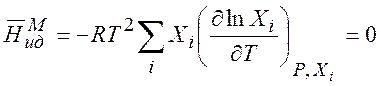                                                                       (7.14)

Найдем объем смешения. Объем одного моля смеси равен

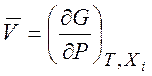
Поэтому

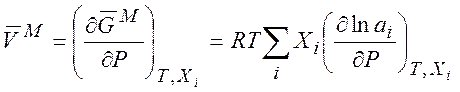                                                                     (7.15)

Найдем энтропию смешения. Учитывая, что

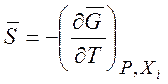
находим

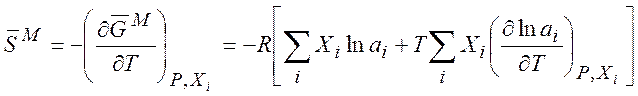                            (7.16)

7.4. Избыточные функции

Избыточная функция - Разница между функцией смешения реальной системы и функцией смешения идеальной системы: