Знаходимо d = 11, s = 11. За даними табл. 7.1 при n = 15 маємо: μ=4,636, σ1=2,153, σ2=1,521. Підставляючи отримані значення у формулу (7.2), розраховуємо значення td і ts, тобто
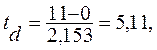
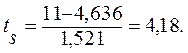
Табличне значення tкр для двостороннього критерію при
n = 15 і рівні значущості ![]() = 0,05 дорівнює
tкр.=2,131451, тобто |td| > tкр,
|ts| > tкр. Отже, гіпотези про відсутність
тенденції у зв'язку між Y і X та
= 0,05 дорівнює
tкр.=2,131451, тобто |td| > tкр,
|ts| > tкр. Отже, гіпотези про відсутність
тенденції у зв'язку між Y і X та ![]() і
Х не підтвердилися, тобто в ряді динаміки експорту простежується деяка
закономірність, проте не можна вважати, що дисперсія постійна й не залежить від
X.
і
Х не підтвердилися, тобто в ряді динаміки експорту простежується деяка
закономірність, проте не можна вважати, що дисперсія постійна й не залежить від
X.
При моделюванні монотонних процесів (зростаючих або спадних), коли число спостережень n невелике, може бути використана одна з таких регресійних функцій, що залежать від двох параметрів:
1) ![]() 2)
2) ![]() 3)
3) ![]()
4)![]() 5)
5)![]() 6)
6)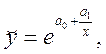
7) 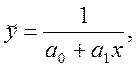 8)
8) 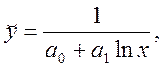 9)
9) 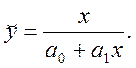
Ці залежності примітні тим, що якщо табличні значення
задовольняють одне із цих рівнянь, то й середні значення ![]() та
та ![]() також
його задовольняють. При цьому в ролі
також
його задовольняють. При цьому в ролі ![]() та
та ![]() може бути середнє арифметичне, геометричне
й гармонічне:
може бути середнє арифметичне, геометричне
й гармонічне:
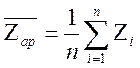 ,
, ![]() ,
,
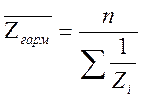 .
.
|
N |
|
|
|
|
Вигляд функції |
|
1 |
х(ар) |
Y(ар) |
|
||
|
2 |
х(геом) |
Y(ар) |
|
||
|
3 |
|
Y(ар) |
|
||
|
4 |
х(ар) |
Y(геом) |
|
||
|
5 |
х(геом) |
Y(геом) |
|
||
|
6 |
х(гарм) |
Y(геом) |
|
||
|
7 |
х(ар) |
y(гарм) |
|
||
|
8 |
х(геом) |
Y(гарм) |
|
||
|
9 |
х(гарм) |
y(гарм) |
|
Для
вибору вигляду функції регресії обчислюють ![]() для
для
![]() у такий спосіб:
у такий спосіб: ![]() =
=![]() , якщо
, якщо ![]() збігається з одним із вузлів xi. Якщо
збігається з одним із вузлів xi. Якщо ![]()
![]() , то
, то 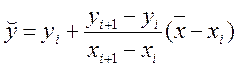 .
.
Як критерій вибору кращої функціональної залежності використовують
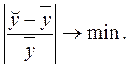
Після того, як обрано вигляд функції, модель перетворюють до лінійного вигляду, якщо це необхідно.
Після того як обрано вигляд функції регресії ![]() , необхідно знайти
невідомі параметри а0, а1, …, аm.
, необхідно знайти
невідомі параметри а0, а1, …, аm.
Метод найменших квадратів полягає в наступному: коефіцієнти а0, а1, …, аm вибираються таким чином, щоб
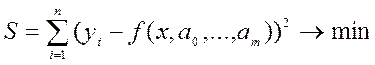 .
.
Сума квадратів відхилень експериментальних значень yi від розрахованих за рівнянням регресії в точках хi повинна бути мінімальною.
Для випадку лінійної функції
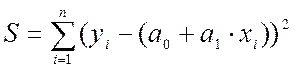 .
.
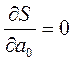 ,
, 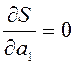 –
необхідна умова існування екстремуму.
–
необхідна умова існування екстремуму.
Отримаємо систему рівнянь
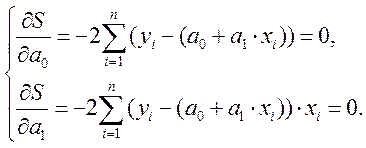 (7.3)
(7.3)
або
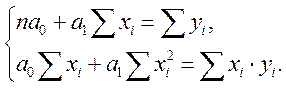
Функція S необмежена зверху, обмежена знизу, має тільки одну критичну точку 1-го роду, може досягати в ній тільки мінімуму.
Розв’язуючи систему рівнянь, знаходимо
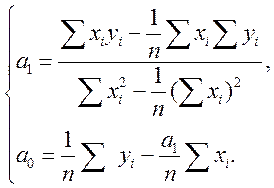
Використовуючи коефіцієнт кореляції, можна записати
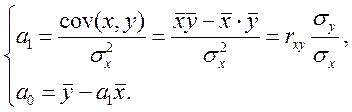 (7.4)
(7.4)
Властивості регресії
1 Регресійна пряма проходить через точку (![]() ).
).
Ми визначили параметри лінійної регресії a1, a0 (7.4), отже рівняння лінійної регресії таке
![]() . (7.5)
. (7.5)
З рівняння (7.4)
![]() . (7.6)
. (7.6)
Віднімаючи від (7.5) рівняння (7.6), отримаємо
![]() . (7.7)
. (7.7)
Отже бачимо, що оцінювана лінія регресії проходить через центр (![]() ). Рівняння (7.7) можна записати у вигляді
). Рівняння (7.7) можна записати у вигляді
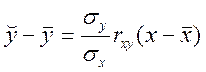 .
.
2
Обчислимо ![]() :
:
![]() .
.
Сума відхилень всіх точок від прямої дорівнює 0. Цю властивість використовують для перевірки обчислень. Розглянемо, з яких частин складаються відхилення рівнянь.
![]() . (7.8)
. (7.8)
У
статистиці різницю ![]() називають загальним
відхиленням заданої випадкової величини.
називають загальним
відхиленням заданої випадкової величини.
![]() – відхилення, які можна
пояснити, виходячи з регресійної залежності. Дійсно, якщо x змінюється,
ці відхилення можна знайти за рівнянням регресії.
– відхилення, які можна
пояснити, виходячи з регресійної залежності. Дійсно, якщо x змінюється,
ці відхилення можна знайти за рівнянням регресії.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.