1. Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса.
Def: Линейная функция: В линейном пространстве L над полем R задана линейная функция (линейная форма), если каждому вектору х Î L поставлено в соответствие число f(x) так, что при этом выполняется следующее: 1) f(x+y)=f(x)+f(y); 2)f(λx)=λf(x)
Def: А(x;y) называется билинейной формой от векторов x,y Î L(вещ.лин.пр-ва), если
1) При фиксированных y A(x;y) – есть линейная функция от х;
a. A(x1+x2;y)=A(x1;y)+A(x2;y)
b. A(λx;y)=λA(x;y)
2) При фиксированных х A(x;y) – есть линейная функция от у
a. А(х;у1+у2)=А(х;у1)+А(х;у2)
b. А(x;λy)=λA(x;y)
Def: Линейная форма называется симметрической, если для все x,yÎL выполняется: A(x;y)=A(y;x) (Скалярное произведение в Евкл. Пространстве является примером симметрической формы).
Выберем в линейном пространстве L базис
e1,e2,…,en и
выразим билинейную форму через координаты αi и βi векторов x,y соответственно в этом базисе. Тогда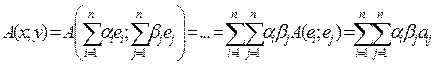 . Где aij=A(ei;ej). Тогда
. Где aij=A(ei;ej). Тогда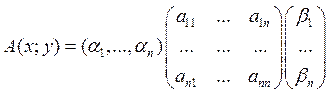 . Где матрица – матрица
билинейной формы A(x;y) в базисе e1,...,en
. Где матрица – матрица
билинейной формы A(x;y) в базисе e1,...,en
Преобразование матрицы билинейной формы при изменении базиса.
Пусть в n-мерном пространстве даны 2 базиса e1,...,en и
f1,...,fn и векторы f выражаются через векторы e с координатами сij.
Тогда матрица С=[сij] (i,j=1..n) – матрица перехода от базиса e к базису f.
С-невырожденная, С-1 – матрица перехода от f к e.
Пусть А=[aik] – матрица билинейной формы в базисе е, а B=[bik] – матрица той же билинейной формы, но в базисе f.
Найдем по матрице А матрицу В.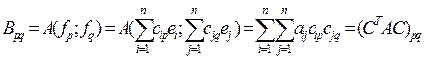 . То есть B=CTAC.
. То есть B=CTAC.
2. Квадратичные формы Приведение квадратичной формы к каноническому виду методом Лагранжа.
Def: Пусть А(х;у) – симметрическая
билинейная форма. Функция А(х;х), которая получается их а(х;у) путем
подстановки y=x называется квадратичной формой. При этом А(х;у)
называется билинейной формой, полярной к А(х;х). Таким образом каждой
симметрической билинейной форме соответствует одна квадратичная форма. Справедливо
и обратное. При заданном базисе всякая квадратичная форма выражается формулой: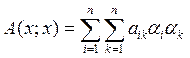 , где aik –
значение билинейной формы A(ei;ek).
, где aik –
значение билинейной формы A(ei;ek).
Def: Квадратичная форма называется положительно определенной, если для x≠0 A(x;x)>0.
Пусть А(х;х) – положительно определенная квадратичная форма, а А(х;у) ее полярная форма. Тогда: 1) А(х;у)=A(y;x) 2)A(x1+x2;y)=A(x1;y)+A(x2;y) 3)A(λx;y)=λA(x;y) 4)A(x;x)=0 ó x=0;
Приведение к сумме квадратов методом Лагранжа.
Покажем как привести квадратичную форму к сумме
квадратов, т.е. выбрать такой базис в котором квадратичная форма имеет наиболее
простой(канонический) вид. А именно:![]() . [Смысл заключается в
поочередном выделении полных квадратов вида (a2+2ab+b2) и
сворачивании их в (a+b)2, а потом замене на другую переменную.
. [Смысл заключается в
поочередном выделении полных квадратов вида (a2+2ab+b2) и
сворачивании их в (a+b)2, а потом замене на другую переменную.
Теорема: Пусть в n-мерном вещественном пространстве L задана произвольная квадратичная форма А(х;х). Тогда в L базис e1,...,en, в котором эта квадратичная форма примет канонический вид. Доказательство: вытекает из самого метода Лагранжа.
3. Приведение квадратичной формы к сумме квадратов методом Якоби.
В отличие от метода Лагранжа мы получим формулы, выражающие искомый базис e через базис f сразу. Пусть мы имеем симметричную форму А(х;у) с матрицей А=||aij||=||A(fi;fj)||. Предположим, что все главные миноры А отличны от нуля(1).(Δ1≠0,...,Δn≠0) Необходимо найти базис e, в котором (2) А(ei;ek)=0 при i≠k. Процесс, с помощью которого это будет сделано напоминает процесс ортогонализации, где в качестве скалярного произведения (х,у) будет выбрано А(х;у). Будем искать векторы ei в виде: ei=αi1f1 + αi2f2+...+αinfn. Заметим, что если A(ek;fi)=0, i=1..k-1, то A(ei,ek)=0. Наша задача свелась к нахождению коэффициентов αki(i=1..k). Т.е. чтобы вектор ek удовлетворял условию (4) A(ek;fi)=0; Этим условиям удовлетворяет вектор ek с точностью до постоянного множителя, который мы зафиксируем условием (5) A(ek;ek)=1. Подставив соотношения 4,5 в выражения для ek получим СЛАУ относительно αki. Определитель этой системы равен Δk и по условию отличен от нуля. Поэтому решение системы существет и единственно. Таким образом задача нахождения вектора ek нами решена для k ; Теперь найдем матрицу В=[bik], которые bik=A(ei;ek) в новом базисе e1,...,en. Во первых, по построению A(ei;ek)=0 при i≠k. Вычислим диагональные элементы bkk. bkk=αkk, где αkk – решения СЛАУ, которые находятся по формуле α = Δk-1/Δk.
Теорема 1.
базис e1,...,en в котором А(х;у) записывается в виде суммы квадратов следующим образом(7):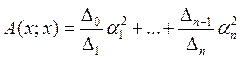 , где α1,...,αn координаты вектора в базисе e1,...,en.
, где α1,...,αn координаты вектора в базисе e1,...,en.
Теорема 2. Число отрицательных коэффициентов при квадратах координат в каноническом виде 7 квадратичной формы равно числу перемен знака в последовательности определителей Δ0,...,Δn .
4. Критерий Сильвестра положительной определенности квадратичной формы. Определители Грамма.
Критерий Сильвестра.
Пусть А(х;у) – симметричная билинейная форма и f1,...,fn – базис n-мерного вещественного пространства L. Для того, чтобы квадратичная форма А(х;х) была положительно определена ó главные миноры были положительны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.