Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 16

Элементарными преобразованиями λ-матриц называются преобразования следующих типов:

1)  Перестановка между собой двух каких-либо строк или столбцов матрицы

2)  Прибавление к строке какой-либо другой строки, умноженной на некоторый многочлен j(λ), и, аналогично, прибавление к столбцу другого столбца, умноженного на некоторый многочлен.

3)  Умножение строки или столбца на некоторое число, отличное от нуля

Теорема: Всякая λ-матрица может быть элементарными преобразованиями приведена к виду

diag(E_i(λ)), i=1,n, где многочлены E_k(λ), стоящие по диагонали, имеют старшие коэффициенты, равные единице, многочлен E₂(λ) делится на E₁(λ), E₃(λ) делится на E₂(λ), E₄(λ) на E₃(λ) и т.д. Этот вид называется нормальной диагональной формой λ-матрицы.

Конечно, некоторое число последних многочленов E_k(λ) в матрице (4) может оказаться равным нулю:  E_r+1(λ) = E_r+2(λ) = … = 0. Мы можем считать, что a₁₁(λ)≠0, так как, если в матрице есть хоть один элемент, отличный от нуля, то перестановками строк и столбцов его можно перевести на это место. Если не все элементы матрицы делятся на a₁₁(λ), то мы можем способом, заменит матрицу эквивалентной, в которой элемент, стоящий в левом верхнем углу, имеет более низкую степень и по-прежнему отличен от нуля. Если не все элементы делятся на него, ты мы можем опять понизить степень этого элемента и т.д. Процесс закончится, когда мы придем к матрице B(λ), в которой все элементы делятся на b₁₁(λ).  Так как элементы b₁₂(λ),…,b_1n(λ) первой строки делятся на b₁₁(λ), то вычитая из второго, третьего и т.д. столбца первый, умноженный на соответственно подобранные многочлены от λ, мы можем обратить в нуль 2-й, 3-й,…,n-й элементы первой строки. Аналогично обратим в нуль все элементы, начиная со второго, в первом столбце. Так как в матрице B(λ) все элементы делились на b₁₁(λ), то в полученной матрице все элементы также делятся на b₁₁(λ). Разделим все элементы первой строки на старший коэффициент многочлена b₁₁(λ). На первом месте получится многочлен со старшим коэффициентом 1, который мы обозначим через  E₁(λ), а на остальных местах будут по-прежнему нули.  Мы пришли, таким образом, к матрице следующего вида:

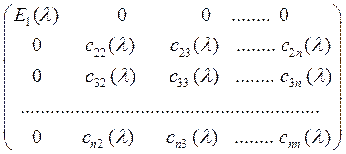все элементы которой делятся на E₁(λ). Мы теперь можем повторить с матрицей (n-1)-го порядка ||c_ik(λ)|| те же операции, что с матрицей n-го порядка. Заметим, что всякое элементарное преобразование матрицы ||с_ik|| есть в то же время элементарное преобразование матрицы (3), так как в первой строке и столбце все элементы, кроме E₁(λ), равны нулю.  Таким образом, мы обратим в нуль все элементы второй строки и второго столбца, кроме диагонального. Полученный диагональный элемент (старший коэффициент которого также считаем равным единице) обозначим E₂(λ).  Все элементы c_ik(λ) делятся на E₁(λ). Поэтому все дальнейшие элементарные преобразования всегда приводят нас к элементам, делящимся на E₁(λ). В частности, E₂(λ) делится на E₁(λ). Мы пришли, таким образом, к матрице у которой в первых двух строках и столбцах все элементы, кроме диагональных, равны нулю, а по диагонали стоят E₁(λ) и E₂(λ), причем E₂(λ) делится на E₁(λ). Мы сможем продолжать этот процесс далее, пока не приведем всю матрицу к диагональному виду. Может, конечно, оказаться, что мы закончим процесс раньше, придя к матрице, состоящей сплошь из нулей.

33. Доказать, что нормальная диагональная форма λ – матрицы определяется однозначно.

Теорема: Нормальная диагональная форма данной λ-матрицы A(λ) определяется по ней однозначно. Если D_k(λ) (k=2,3,…,r) – наибольший общий делитель миноров k-го порядка матрицы A(λ), а D_r+1(λ) = … = D_n(λ) = 0, то элементы нормальной диагональной формы определяются по формулам

E_k(λ) = 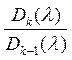 (k=1,2,…,r)

E_r+1(λ) = E_r+2(λ) = … = E_n(λ) = 0

Доказательство: Мы показали, что при элементарных преобразованиях многочлены D_k(λ) не меняются. Поэтому, если матрица A(λ) эквивалентна диагональной нормальной матрице, то D_k(λ) у них совпадают. Так как для матрицы мы получили, что D_k(λ) = E₁(λ)…E_k(λ)   (k=1,2,…,r ; r<=n) и что D_r+1(λ) = D_r+2(λ) = … = D_n(λ) = 0, то теорема доказана

34-36. Вычисление функции от матрицы.