Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 9

1)  ортогональный оператор сохраняет длины векторов;

2)  ортогональный оператор сохраняет углы между векторами.
Доказательство.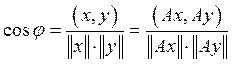

3)  Если  - ортонормированный базис в Х, то  тоже образуют ортонормированный базис в Х.
Доказательство.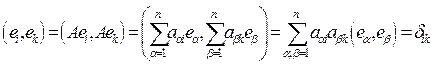

4)  Матрица  ортогонального оператора в ортонормированном базисе имеет ортонормированные строки и столбцы.

5)  Определитель матрицы ортонормированного оператора равен.
Доказательство..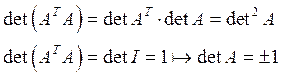

6)  Ортогональный оператор всегда не вырожден.

7)  Тождественный оператор является ортогональным.

8)  Произведение ортогональных операторов снова будет ортогональным оператором.
Доказательство.

9)  Оператор, обратный ортогональному, тоже ортогональный.
Доказательство..

10)  Линейный оператор, переводящий хотя бы один базис в ортонормированный, является ортогональным.
Доказательство.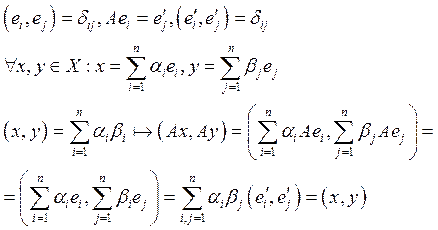

Определение. Ортогональные операторы, определитель матрицы которых равен 1, называются собственными, у которых равен –1, несобственными.

Лемма 3. Если  - подпространство евклидова пространства Х, инвариантное относительно ортогонального оператора А, то его ортогональное дополнение  также является инвариантным пространством.

Доказательство. Если взять. Поскольку А – ортогональный оператор, он не вырожден и его образ на любом инвариантном подпространстве совпадает с этим пространством, поэтому х имеет свой прообраз.

Теорема 4. Матрица ортогонального оператора в некотором ортонормированном базисе имеет вид:

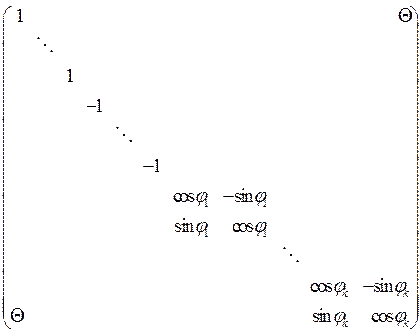
Доказательство. По теореме 1 (билет 16) любой линейный оператор в n-мерном евклидовом пространстве имеет одномерное или двумерное инвариантное подпространство. Если  - одномерное и инвариантное относительно нашего линейного оператора пространство, то найдем е, порождающий. На этом подпространстве линейный оператор имеет вид. Если же  - двумерное пространство и определитель А является собственным оператором, то имеет матрицу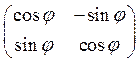. По лемме 3, ортогональное дополнение  будет также инвариантным относительно ортогонального оператора А. Рассмотрим действие А на ортогональное дополнение, и, проведя точно такой же анализ, мы получим еще одномерное и двумерное подпространство. Продолжая этот процесс, получим ортонормированный базис, в котором матрица ортогонального оператора имеет требуемую структуру. 1 и –1 отвечают одномерным инвариантным пространствам, а клетки с  соответствуют двумерным инвариантным пространствам.

19. Определение аффинного пространства. Различные способы задания прямой в аффинном пространстве (векторный, в параметрическом виде, канонический, по двум точкам). Угол между прямыми. Нахождение расстояния от данной точки до данной прямой.  Перпендикуляр, опущенный из точки на прямую.

Def:  пусть задано n-мерное векторное пространство Vⁿ над полем F и непустое множество Aⁿ, элементы которого будем называть точками. Предположим, что  упорядоченной паре точек M,N Π Aⁿ поставлен в соответствие вектор пространства Vⁿ, обозначаемый, причем выполнены следующие аксиомы:

1)Для  M Î Aⁿ и  a Π Vⁿ   единственная точка N Π Aⁿ, что =a 2) Для  трех точек L,M,N Π Aⁿ имеет место.

Тогда множество Aⁿ называется n-мерным аффинным пространством, связанным с векторным пространством Vⁿ.

Способы задания прямой:

Def: Будем называть прямой в аффинном пространстве множество точек этого пространства, получаемых из одной его точки всеми переносам, векторы которых коллинеарны. Т.к. векторы этих переносов имеют вид at, где t Î R, радиус-векторы прямой имеют вид (1)x=x₀+at.

1)  Уравнение 1 называется векторным уравнением прямой. При этом а – направляющий вектор. Две различные прямые, полученные из различных точек одними и теми же переносами, называются параллельными.

2)  Координатные уравнения прямой. Уравнение 1 равносильно n координатным уравнениям (2) x_i=x₀+a_it. Уравнение 2 – параметрическое уравнение прямой. Разрешая его относительно T и приравнивая полученные выражения получаем: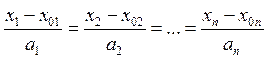 - каноническое уравнение прямой.