Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 10

3)  Уравнение прямой по двум точкам. Если задано две точки M₀(x₀) и M₁(x₁), то за направляющий вектор прямой, проходящей через эти две точки можно принять =x₁-x₀ . Поэтому векторное уравнение этой прямой может быть записано в виде x=x₀+(x₁-x₀)t, а каноническое уравнение: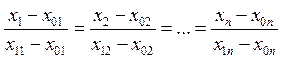

Расстояние от точки до прямой. Расстояние w от точки M(r) до произвольной точки прямой определяется соотношением (7): . Исследуя w² как функцию от t. (8)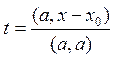 - это значение даст минимальное расстояние. Подставляя 8 в 7 получаем: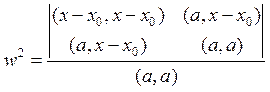

Перпендикуляр, опущенный из точки на прямую. Требуя, чтобы отрезок MN, соединяющий М(х) с некоторой точкой N прямой, был перпендикулярен направляющему вектору а этой прямой, т.е. чтобы вектор x-x₀-at был ортогонален а. (x-x₀-at,a)=0. Значение t, удовлетворяющее этому условию совпадает с 8. Это совпадение |-> основание N перпендикуляра, опущенного из данной точки М на прямую, совпадает с той точкой прямой, которая находится на минимальном расстоянии от данной точки.

20. Взаимное расположение двух прямых. Нахождение кратчайшего расстояния между двумя скрещивающимися прямыми. Общий перпендикуляр двух прямых.

Взаимное расположение двух прямых. Если две прямые в n-мерном аффинном пространстве, определяющиеся уравнениями  (10) пересекаются (имеют одну общую точку), т.е. существуют такие значения t и u, когда. Т.е. линейно независимы. Если две прямые, заданные уравнения (10) параллельны и их направляющие векторы а, b коллинеарны, т.е.. Т.о. опять линейно зависимы. Покажем, что справедливо обратное, т.е. если векторы  линейно зависимы, то прямые (10) пересекаются или параллельны. Действительно, если, то прямые  параллельны; если же векторы а и b неколлинеарны, то вектор  может быть представлен в виде линейной комбинации векторов а и b, т.е. в виде:. Поэтому точка, радиус-вектором которой является этот вектор, есть точка пересечения данных прямых. Т.о. необходимым и достаточным условием того, что две прямые, заданные выражением (10), пересекаются или параллельны, является линейная зависимость тройки векторов. Если же вышеописанная тройка линейно независима, то прямые скрещиваются.

Кратчайшее расстояние между двумя скрещивающимися прямыми. Найдем кратчайшее расстояние между двумя скрещивающимися прямыми l и m, которые записаны уравнением (10):

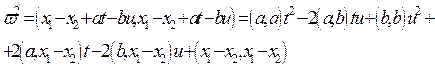(13)

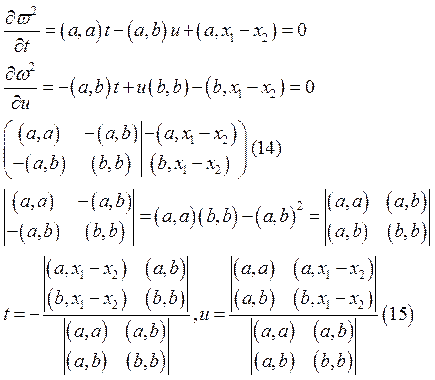
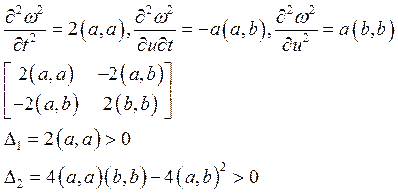
Вектор MN имеет вид: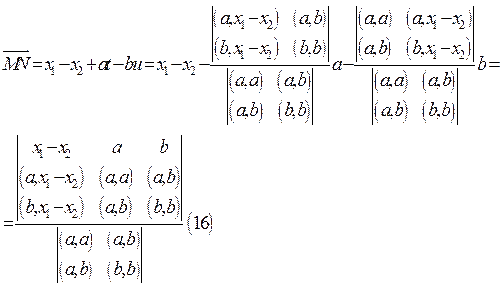 

Вычислим теперь: 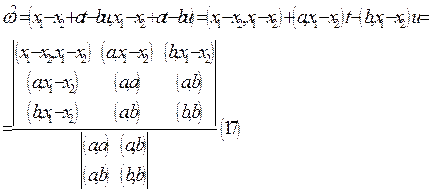Общий перпендикуляр двух прямых. Требуем, чтобы отрезок, соединяющий произвольные точки двух данных прямых (10), был перпендикулярен направляющим векторам а и b обеих прямых. Мы получили условие (14), отсюда находим, что значение t и u, удовлетворяющие этому условию, совпадают со значением (15). Это совпадение показывает, что основания общего перпендикуляра двух прямых совпадают с теми точками эти прямых, расстояние между которыми минимально.

21. Различные способы задания плоскостей (векторный, в параметрическом виде, по точке и нормали, по точке и направляющим векторам, по n точкам). Основная теорема о плоскости. Угол между плоскостями. Условие принадлежности n+1 точки одной плоскости.

Определение. Будем называть m-мерной плоскостью аффинного пространства или m-плоскостью множество всех точек этого пространства, полученных из одной его точки всеми переносами, векторы которых коллинеарны и принадлежат одному линейному пространству.

Т.к. векторы этих переносов имеют вида, где  принимает все вещественные значения, то радиус-векторы точек m-плоскости имеют вид? 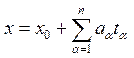(1) – векторное уравнение m-плоскости. Векторы  называются направляющими векторами m-плоскости.

Замечание. Прямые можно рассматривать, как 1-плоскость; точки – как 0-плоскость.

Определение. Различные плоскости, получающиеся из различных точек одними и теми же переносами, называются параллельными плоскостями. ().

Уравнение (1) равносильно 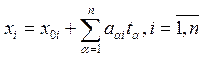 (2) – параметрическое (координатное) уравнение m-плоскости в координатах.

Если задано m+1 точек  и векторы  линейно независимы, то эти точки определяют единственную m-плоскость, проходящую через них. В этом случае за направляющие векторы этой плоскости можно принять векторы  , и векторное уравнение m-плоскости может быть записано в виде: 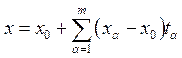(3).