Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 4

Эквивалентные и подобные матрицы.

Def: 2 прямоугольные матрицы  А,В одинаковой размерности называются эквивалентными, если  2 невырожденных квадратных матрицы R и S, что  B=RAS

Из соотношения 7 |-> две матрицы, соответствующие одному и тому же линейному оператору, эквивалентны между собой. Справедливо и обратное: если А отвечает некоторому оператору А в базисах Х и Y, а матрица В эквивалентна А, то она отвечает тому же линейному опреаторув некоторых других базисах Х и Y.

Теорема. Критерий эквивалентности двух матриц.

Для того, чтобы две прямоугольные матрицы одинаковых размеров были эквивалентными ó чтобы они имели один и тот же ранг.

Доказательство : -> Ранг произведения двух матриц не превосходит ранга любой из них. При умножении какой-либо матрицы на невырожденную матрицу ранг ее не меняется, поэтому эквивалентные матрицы имеют один и тот же ранг. Можно показать и обратное, что матрицы одинаковых рангов эквивалентны между собой. Мы докажем, что всякая матрица ранга r эквивалентна I_r(единичной матрице размерности r). Пусть дана прямоугольная матрица размера nxm . Она определяет некоторый линейный оператор А, отображающий пространство Х с базисом е в пространство Y с базисом g. Обозначим через r число линейно независимых векторов среди образов векторов базиса Ae₁,...,Ae_n. Не нарушая общности можно считать, что линейно независимыми являются векторы Ae₁,...,Ae_r. Остальные векторы выражаются через них. Определим новый базис следующим образом: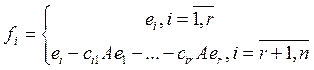. Тогда, если мы возьмем и рассмотрим образ i-го базисного вектора f, то Afi=θ для  i=r+1,n. Векторы h1...hr – линейно независимы, а это векторы из Y. Дополним их некоторыми векторами h_r+1,...,h­­_m До базиса в линейном пространстве Y. И рассмотрим матрицу оператора А в новых базисах f₁...f_n и h₁...h_m. Коэффициенты i-го столбца этой матрицы совпадает с коэффициентами вектора Af_i в базисе h . Согласно соотношениям матрица А будет совпадать с матрицей I_r. Т.к. А и Ir соответствуют одному и тому же оператору, то они эквивалентны.

Def:  А называется подобной матрице B если существует такая невырожденная матрица P, что A=P^-1BP. 1) Если А подобна В, то В подобна А. 2)Если А подобна В, а В подобна С, то А подобна С. Поскольку признак подобия удовлетворяет условиям рефлексивности, симметричности и транзитивности, он является отношением эквивалентности.

10.  Инвариантные подпространства. Собственные векторы и собственные значения линейного оператора. Доказать, что в комплексном линейном пространстве всякий линейный оператор имеет хотя бы один собственный вектор.

Def: Подпространство L линейного пространства X называется инвариантным, относительно А, если для xÎL верно: AxÎL. Всякий линейный оператор имеет по крайней мере 2 тривиальных инвариантных подпространства: 1) Нулевое подпространство 2) Все пространство Х.

Пусть L₁ – одномерное подпространство, порожденное ненулевым вектором Х. Ясно, что для того, чтобы L₁ было инвариантным ó Ax Î L₁. Ax=λx;

Def:  Вектор х ≠ θ, удовлетворяющий Ax=λx называется собственным вектором, а соответствующее ему число λ  - собственным значением. Все отличные от нуля векторы инвариантного подпространства являются собственными.

Теорема. В комплексном линейном пространстве Х линейный оператор имеет хотя бы один собственный вектор.

Доказательство.  Пусть в линейном пространстве Х выбран базис e₁,...,e_n . В этом базисе А соответствует матрица Ае=[a_ij]. Выберем произвольный х Î Х. х = α₁e₁+...+ α_ne_n. А координаты β выражаются формулами:.. Переносим и группируем. Для доказательства теоремы нужо показать, что  λ и числа α₁,...,α_n не все равные нулю, удовлетворяющие системе 2. Условием существования ненулевого решения системы 2 является равенство нулю ее определителя. det(A-λI)=0. Мы получили уравнение n-ой степени, относительно λ. Это уравнение имеет хотя бы один корень (в общем случае комплексный) λ₀­. Подставив в систему 2 вместо λ λ₀­ получим однородную СЛАУ с нулевым определителем, имеющую ненулевое решение. Тогда вектор х, удовлетворяющий этому решению будет собственным вектором, соответствующим собственному значению λ_0.