Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 15

Если вместо преобразования A рассмотреть преобразование A+λI, то, так как матрица преобразования λI диагональная, мы получим тот же результат для преобразования пространства R, имеющего только одно собственное значение равное произвольному числу λ₁. Соответствующие жордановы клетки матрицы преобразования A+λ₁I будут иметь вид: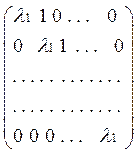

Вспоминая теперь, что для произвольного преобразования A мы можем разложить пространство R в сумму инвариантных подпространств, в каждом из которых преобразование A имеет только одно собственное значение.

31. Теорема о жордановой нормальной форме линейного оператора и основные этапы ее доказательства.

Пусть задано произвольное линейное преобразование A в комплексном пространстве n измерений. Предположим, что у A имеется k (k<=n) линейно независимых собственных векторов e₁,f₁,…,h₁, соответствующих собственным значениям λ₁,λ₂,…,λ_k. Тогда существует базис, состоящий из k групп векторов:

e₁,…,e_p ; f₁,…,f_q; … ; h₁,…,h_s, (1)

в котором преобразование A имеет вид:

Ae₁ = λ₁e₁,   Ae₂ = e₁ + λ₁e₂,   …   ,   Ae_p = e_p-1 + λ₁ e_p      (2)

Af₁ = λ₂f₁,    Af₂ = f₁ + λ₂f₂,    …   ,   Af_q = f_q-1 + λ₂ f_q

……………………………………………………….

Ah₁ = λ_kh₁,  Ah₂ = h₁ + λ_kh₂,  …   ,   Ah_s = h_s-1 + λ_kh_s  

Мы видим, что базисные векторы каждой группы переходят при нашем преобразовании в линейную комбинацию векторов той же группы. Отсюда следует, что каждая группа базисных векторов порождает подпространство, инвариантное относительно преобразования A. Рассмотрим несколько подробнее преобразование, задаваемое формулами (2).

В подпространстве, порожденном каждой группой, есть собственный вектор, например, в подпространстве, порожденном векторами e₁,e₂,…,e_p, таким собственным вектором является e₁.

Вектор e₂ называют иногда присоединенным вектором первого порядка. Это значит, что Ae₂ пропорционально e₂ с точностью до собственного вектора, как это видно из равенства

Ae₂ = λ₁e₂ + e₁

Аналогично e₃,e₄,… называют присоединенным векторами второго, третьего и т.д. порядков

Каждый из них является «как бы собственным», т.е. собственным с точностью до присоединенного вектора низшего порядка

Ae_k = λ₁e_k + e_k-1

Таким образом, базис каждого инвариантного подпространства состоит из одного собственного вектора и такого же количества присоединенных векторов, которое нужно добавить, чтобы получить базис данного подпространства.

Покажем, что в каждом из этих подпространств имеется, c точностью до множителя, лишь один собственный вектор.

Выпишем матрицу преобразования (2). Так как векторы каждой группы преобразуются в линейные комбинации векторов той же группы, то в первых p столбцах матрицы преобразования могут быть отличны от нуля лишь элементы первых p строк, в следующих q столбцах могут быть отличны от нуля лишь элементы, стоящие в строках с теми же номерами, что и у этих столбцов, и т.д. Таким образом, в данном базисе матрица преобразования будет состоять из k клеток, расположенных по главной диагонали, а все элементы, не принадлежащие ни одной из этих клеток, будут равны нулю.

Для того, чтобы понять, что стоит в каждой клетке матрицы преобразования, достаточно еще раз написать, как преобразуются векторы одной группы. Мы имеем:

Ae₁ = λ₁e₁,

Ae₂ = e₁ + λ₁e₂,

………………………………………..

Ae_p-1 = e_p-2 + λe_p-1,

Ae_p = e_p-1 + λ₁e_p.

Вспоминая, как строится матрица, отвечающая данному преобразованию базиса, получаем, что клетка матрицы, соответствующая данной группе векторов, имеет вид 1

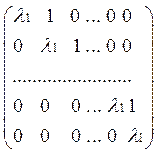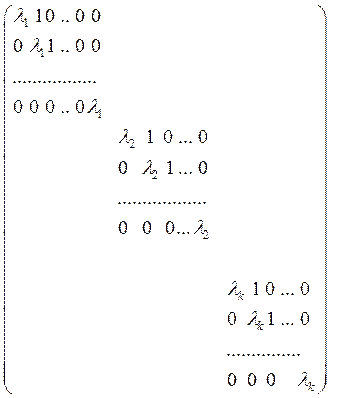 (1) (2)

Вся же матрица оказывается составленной из таких клеток порядков p,q,…,s соответственно, т.е. имеет вид 2, где все элементы вне клеток – нули.

Заметим также, что не все λ_i обязаны быть различными.

32. λ – матрицы. Элементарные преобразования λ – матриц. Доказать, что всякую λ – матрицу путем элементарных преобразований можно привести к нормальной диагональной форме.

Def: λ – матрицей называется матрица, элементами которой являются многочлены относительно некоторой буквы λ. Степенью λ – матрицы называется наивысшая из степеней многочленов, входящих в состав матрицы.