Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 7

3)  В ортонормированном базисе строки и столбцы матрицы унитарного оператора U ортонормированные.

4)  Рассмотрим скалярное произведение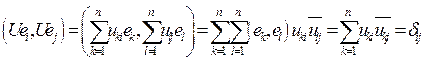. Следовательно, для того, чтобы линейный оператор U был унитарным необходимо и достаточно, чтобы он переводил какой-либо ортонормированный базим  в ортонормированный базис.

Определение. Матрица с элементами, удовлетворяющая условиям (3, 4), называется унитарной матрицей.

Замечание. Т.к. переход от одного ортонормированного базиса к другому осуществляется унитарным оператором, матрица перехода от одного ортонормированного базиса к другому такому же является унитарной.

Лемма 1. Собственные значение унитарного оператора по модулю равны 1 (лежат на окружности единичного радиуса).

Доказательство. Пусть х – собственный вектор унитарного оператора U и  - соответствующее собственное значение:. Рассмотрим

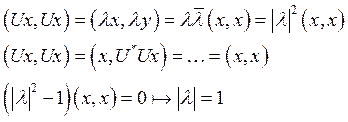
Лемма 2. Пусть унитарный оператор U, действующий в n-мерном пространстве Х, а е – его собственный вектор. Тогда (n-1)-мерное пространство, состоящее из векторов  инвариантно относительно U.

Доказательство. пространство  инвариантно.

Теорема 1. Для любого унитарного оператора в n-мерном пространстве существует n попарно ортогональных собственных векторов, соответствующие им собственные значения по модулю равны 1.

Доказательство. Унитарный оператор U имеет в Х хотя бы один собственный вектор, обозначим его через. По лемме 2 (n-1)-мерное подпространство, состоящее из всех векторов пространства Х ортогональных к, инвариантно относительно унитарного оператора U. Продолжая это процесс, мы получим n попарно ортогональных собственных векторов  унитарного оператора U. По лемме 1 собственные значения, соответствующие собственным векторам, по модулю равны 1.

Теорема 2. Для любого унитарного оператора U в n-мерном пространстве Х существует ортонормированный базис, в котором матрица этого оператора диагональна: (5).

Доказательство. Пусть U – унитарный оператор, тогда по теореме 1 существует ортонормированный базис пространства Х из собственных векторов унитарного оператора U:. В этом базисе матрица U имеет вид (5), а числа  в силу леммы 1.

15. Спектральная характеристика нормального оператора. Критерий простоты структуры линейного оператора.

Определение. Линейный оператор  называется нормальным, если.

Замечание. Унитарные и самосопряженный линейные операторы являются частными случаями нормальных операторов.

Теорема. Спектральная характеристика нормального оператора. Для того, чтобы существовал ортонормированный базис, в котором линейный оператор приводится к диагональной форме, необходимо и достаточно, чтобы.

Доказательство.

Необходимость. Пусть в некотором ортонормированном базисе матрица оператора А диагональна, т.к. базис ортонормированный, то матрица оператора  будет  (транспонирование, сопряжение). Следовательно,.

Достаточность. Пусть. Покажем, что у операторов А и  существует общий собственный вектор:

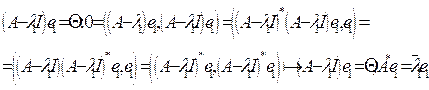Линейная оболочка  будет одномерным инвариантным подпространством, а  будет также инвариантным подпространством. Докажем это:

Пусть.  также будет принадлежать, т.к.. Рассмотрим теперь действие оператора А из  ()… Продолжая этот процесс, получим ортогональный базис из собственных векторов, нормируем его – нормированный.

Определение. называется оператором простой структуры, если А имеет n линейно независимых собственных векторов.

Теорема. Критерий простоты структуры линейного оператора. Для того, чтобы линейный оператор А имел простую структуру необходимо и достаточно, чтобы для любого корня  характеристического уравнения кратности  ранг.

Доказательство.

Необходимость. А – оператор простой структуры. Следовательно, существуют n линейно независимых векторов, выбирая которые в качестве базиса L, получим, что матрица линейного оператора в базисе  имеет вид:. Причем среди  могут быть одинаковые. Если через А обозначить матрицу линейного оператора в некотором произвольном базисе, то, где Р – матрица перехода от базиса е из собственных векторов к базису f. Следовательно, т.е. и  подобны и имеют одинаковый ранг.. числу отличных от нуля ее диагональных элементов, т.е. числу корней характеристического уравнения неравных, т.о..