Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 2

Доказательство: -> Пусть А(х;х) – положительно определенная квадратичная форма. Покажем, что главный минор Δk>0. Предположим, что Δk=0. Тогда одна из строк есть лиейная комбинация остальных. То есть их линейная комбинация может быть равна нулю при неравных нулю коэффициентах μ_i . Тогда (выписывая коэффициенты при μ) μ₁A(f₁;f_i)+...+μ_kA(f­_k,f_i)=0 для  i=1..k.

A(μ₁f₁+...μ_kf_k;f_i)=0

A(μ₁f₁+...μ_kf_k; μ₁f₁+...μ_kf_k)=0. Значит μ₁f₁+...μ_kf_k=0. Противоречие, значит Δk ≠ 0 и А(x;x) можно привести к каноническому виду. Где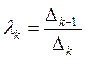. Отсюда, λ₁>0(Δ₁>0), λ₂>0(Δ₁>0,Δ­₂>0),...

<- Если Δ₁>0,... то  базис e₁,...,e_n  в котором квадратичная форма имеет канонический вид. Причем все λ_i >0/ Следовательно А(х;х)>0 для всех х. Т.е. Ах;х) – положительно определенная квадратичная форма.

Определители Грамма.

Выберем в качестве квадратичной формы скалярное произведение А(х;х)=(х,х). Пусть e₁,...,e_n – векторы в пространстве  E. Тогда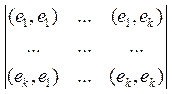- определитель Грамма.

Теорема. Определитель Грамма любой системы векторов всегда ≥0. Причем =0 ó e₁,...,e_k - линейно зависимы.

Доказательство: Пусть e₁,...,e_k  - линейно независимы. Рассмотрим А(х;у)=(х,у). Тогда определитель Грамма есть определитель матрицы B=[α_ij]=[A(e_i;e_j)]. ΔB = Δk. Т.к. А(х;х) – положительно определенная квадратичная форма, то из критерия Сильвестра: Δk>0. Если e₁,...,e_k – линейно зависимы, то одна из строк есть линейная комбинация всех остальных, значит определитель Грамма равен нулю.

5.  Закон инерции квадратичной формы. Ранг квадратичной формы.

Теорема. Если квадратичная форма приведена двумя различными способами (в двух различных базисах) к сумме квадратов, то число положительных, отрицательных и нулевых коэффициентов в обоих случая одно и то же.

Доказательство. Пусть в базисе  квадратичная форма  имеет вид: (1), где  - координаты вектора х, т.е.. Пусть в базисе  эта квадратичная форма имеет вид: (2), где  - координаты вектора х в базисе. Нужно доказать, что . Докажем это от противного. Предположим, что. Рассмотрим подпространство,. Т.к., то существует ненулевой вектор х, принадлежащий пересечению:. Тогда. В базисе е вектор х имеет координаты, а в базисе f -. Подставляя эти представления в формулы (1, 2), мы получаем с одной стороны, что  (т.к. не все числа  равны нулю). Если подставить в формулу (2), то имеем, что  (Т.к. хотя среди чисел  есть отличные от нуля, возможно, что). Противоречие, следовательно, неравенство  неверно. Аналогично доказывается, что невозможны неравенства.

Определение. Число r, отличных от нуля коэффициентов  в каноническом виде квадратичной формы называется рангом квадратичной формы.

Чтобы найти ранг квадратичной формы нужно вычислить ранг ее матрицы в какой-либо одной системе координат.

Определение.  Назовем число положительных  и число отрицательных  коэффициентов в каноническом виде квадратичной формы соответственно положительными и отрицательными индексами инерции:.

Определение. Если, то квадратичная форма называется невырожденной. Разность между положительными и отрицательными индексами инерции называется сигнатурой.

6.  Определение и примеры линейных операторов. Действия с линейными операторами. Пространство линейных операторов.

Определение. Пусть Х и У – линейные пространства, заданные на одним и тем же полем F. Правило, по которому каждому элементу  ставится в соответствие единственный элемент, называется оператором или преобразованием. Результат применения оператора  обозначают.

Определение. Запись  значит, что оператор А действует из Х в У или отображает Х в У. При этом Х называется областью определения оператора А, у – образом элемента х, а х – прообраз у.

Определение. Образ оператора А или область его значений это совокупность всех элементов  таких, что:.

Определение. Оператор А с областью определения Х и областью значений У называется линейным оператором, если он линейной комбинацией прообразов ставит в соответствие линейную комбинацию образов..

Определение. Если, то линейный оператор называется оператором в Х.

Определение. Операторы А и В называются равными (А=В) тогда и только тогда, когда.