Жорданова нормальная форма линейного оператора

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Расчетно-графическое задание

по теме «Жорданова нормальная форма
линейного оператора»

Факультет:                 ПМИ

Группа:                      ПМ-22

Студент:                     Рембиш Алексей

Преподаватель: Чубич Владимир Михайлович

Вариант:                    21

Новосибирск, 2003

Задание

Цель задания: ознакомление с понятием жордановой формы (ЖНФ), приобретение практических навыков построения ЖНФ линейного оператора, заданного своей матрицей.

Срок выполнения: две недели.

Время защиты: по указанию преподавателя.

Вариант: 21.

Матрица: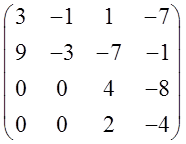

Решение

Пусть в некотором базисе линейный оператор имеет матрицу

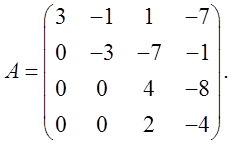
Найдем собственные значения матрицы :

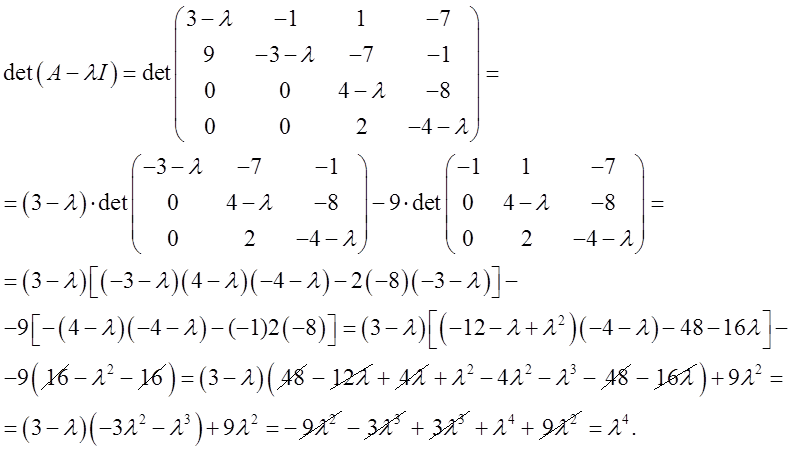
Таким образом, матрица  имеет одно собственное значение , алгебраическая кратность которого . Определи геометрическую кратность собственного значения по формуле .

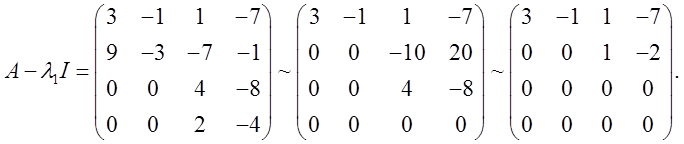
Отсюда .

Получаем, что четырехмерное пространство  распадается на прямую сумму двух корневых подпространств и, как следствие, матрица  имеет два собственных вектора. В данный момент, нельзя точно указать какими будут два оставшихся присоединенных вектора: присоединенный первого порядка и присоединенный второго порядка или два присоединенных первого порядка.

Мы получили общий вид двух различных собственных векторов:

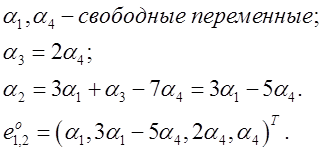
Теперь осталось найти присоединенные векторы. Для этого решим неоднородную СЛАУ, если при ее решении мы не получим ограничений, связанных с совместностью СЛАУ (по теореме Кронекера-Капелли), то мы имеем два присоединенных вектора первого порядка, иначе – по одному первого и второго порядков.

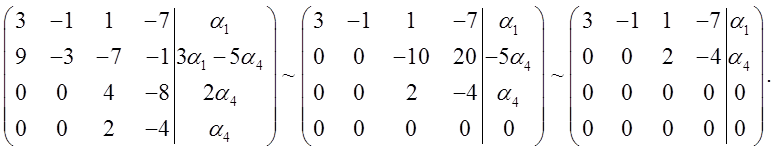
Ограничений при решении СЛАУ не получили, следовательно,  и матрица  имеет два различных присоединенных вектора первого порядка (у каждого из собственных векторов). Найдем их общий вид:

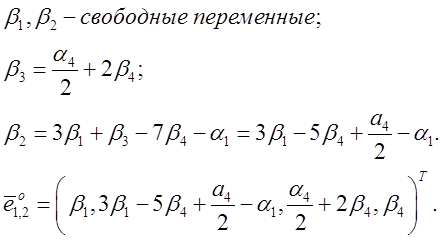
Теперь выберем значения свободных переменных:

	0

Отсюда получаем:

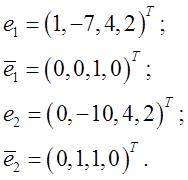
Таким образом, построен канонический базис, состоящий из следующей последовательности жордановых цепочек:

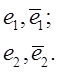
Поскольку жордановой цепочке длины  отвечает клетка порядка , то ЖНФ матрицы  имеет вид:

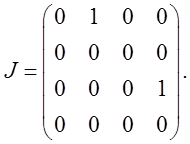
Проверим правильность полученных результатов. В силу того, что матрицы  и  подобны как матрицы одного линейного оператора в различных базисах, то должно выполняться равенство , где матрица  - матрица перехода от исходного базиса к найденному каноническому. Поскольку столбцами матрицы  являются векторы канонического базиса , то получаем:

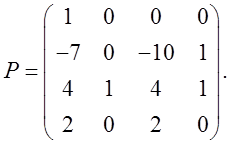
Отсюда получим :

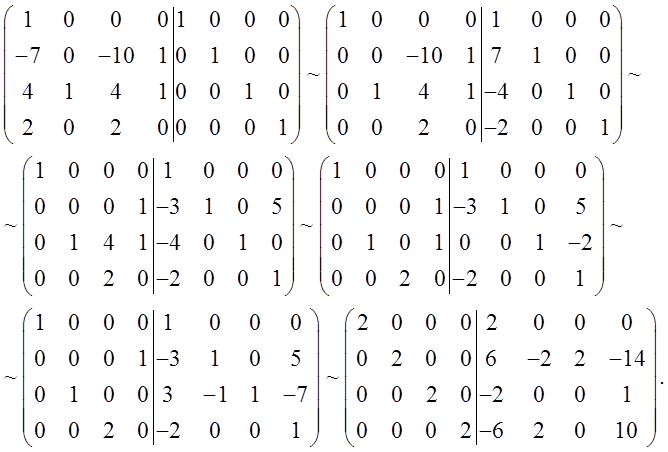
Получили, что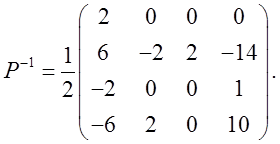  

Проверим:

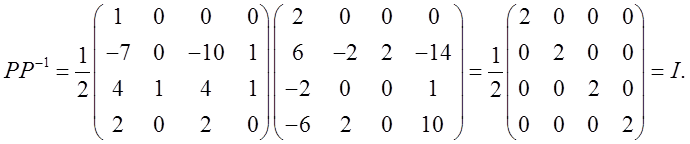
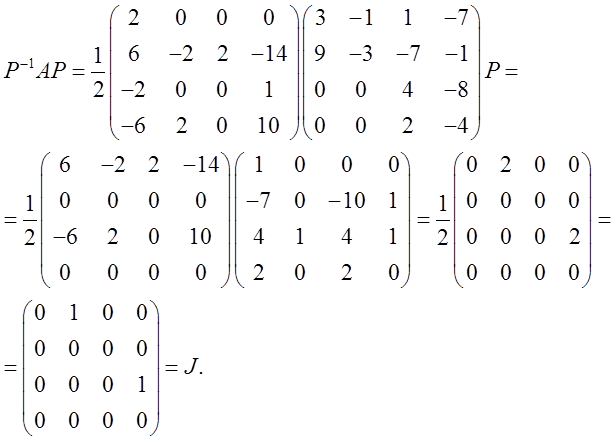
Проверка показала правильность решения.