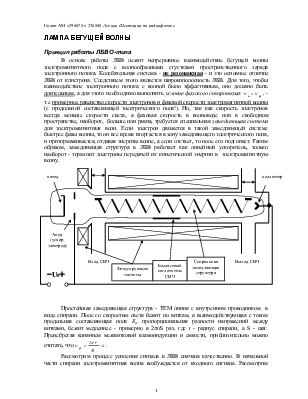













В основе работы ЛБВ лежит непрерывное взаимодействие
бегущей волны электромагнитного поля с волнообразными сгустками
пространственного заряда электронного потока. Колебательная система - не
резонансная - и это основное отличие ЛБВ от клистрона. Следствием этого
является широкополосность ЛБВ. Для того, чтобы взаимодействие электронного
потока с волной было эффективным, оно должно быть длительным, а для
этого необходимо выполнить условие фазового синхронизма: ![]() , - т.е примерное
равенство скорости электронов и фазовой скорости электромагнитной волны (с
продольной составляющей электрического поля!). Но, так как скорость электронов
всегда меньше скорости света, а фазовая скорость в волноводе или в свободном
пространстве, наоборот, больше или равна, требуется специальная замедляющая
система для электромагнитных волн. Если электрон движется в такой
замедляющей системе быстрее фазы волны, то он все время вторгается в зону
замедляющего электрического поля, и притормаживается, отдавая энергию волне, а
если отстает, то поле его подгоняет. Таким образом, замедляющая структура в ЛБВ
работает как линейный ускоритель, только наоборот - тормозит электроны
передачей их кинетической энергии в электромагнитную волну.
, - т.е примерное
равенство скорости электронов и фазовой скорости электромагнитной волны (с
продольной составляющей электрического поля!). Но, так как скорость электронов
всегда меньше скорости света, а фазовая скорость в волноводе или в свободном
пространстве, наоборот, больше или равна, требуется специальная замедляющая
система для электромагнитных волн. Если электрон движется в такой
замедляющей системе быстрее фазы волны, то он все время вторгается в зону
замедляющего электрического поля, и притормаживается, отдавая энергию волне, а
если отстает, то поле его подгоняет. Таким образом, замедляющая структура в ЛБВ
работает как линейный ускоритель, только наоборот - тормозит электроны
передачей их кинетической энергии в электромагнитную волну.
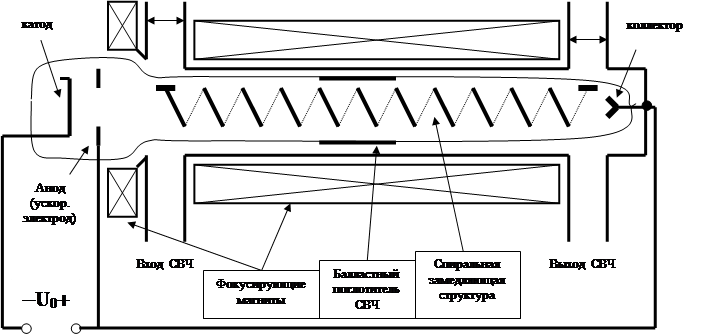
Простейшая замедляющая структура - ТЕМ линия с
внутренним проводником в виде спирали. Поле со скоростью света бежит по
виткам, а взаимодействующая с током продольная составляющая поля Ez, пропорциональная разности напряжений между витками,
бежит медленнее - примерно в 2pr/S раз, где r - радиус спирали, а S - шаг.
Пренебрегая влиянием межвитковой взамоиндукции и
емкости, приблизительно можно считать, что ![]() .
.
Рассмотрим процесс усиления сигнала в ЛБВ сначала
качественно. В начальной части спирали электромагнитная волна возбуждается от
входного сигнала. Рассмотрим распределение продольного электрического поля,
движущееся вместе с волной вдоль замедляющей структуры со скоростью ![]() в системе
координат, сопутствующей фазе:
в системе
координат, сопутствующей фазе:
![]() .
.
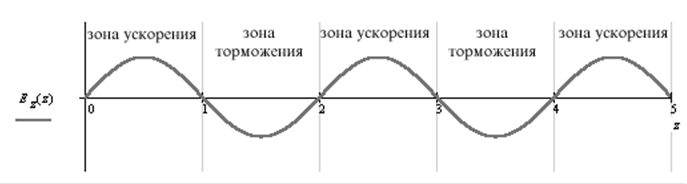
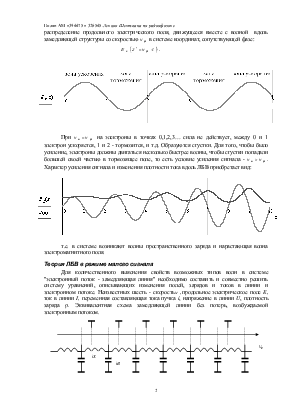
При ![]() на
электроны в точках 0,1,2,3… сила не действует, между 0 и 1 электрон ускоряется,
1 и 2 - тормозится, и т.д. Образуются сгустки. Для
того, чтобы было усиление, электроны должны двигаться несколько быстрее волны,
чтобы сгустки попадали большей своей частью в тормозящее поле, то есть условие
усиления сигнала -
на
электроны в точках 0,1,2,3… сила не действует, между 0 и 1 электрон ускоряется,
1 и 2 - тормозится, и т.д. Образуются сгустки. Для
того, чтобы было усиление, электроны должны двигаться несколько быстрее волны,
чтобы сгустки попадали большей своей частью в тормозящее поле, то есть условие
усиления сигнала - ![]() .
Характер усиления сигнала и изменения плотности тока вдоль ЛБВ приобретает вид:
.
Характер усиления сигнала и изменения плотности тока вдоль ЛБВ приобретает вид:
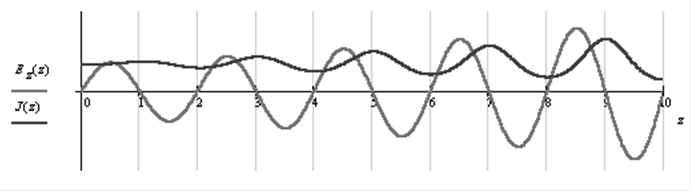
т.е. в системе возникают волны пространственного заряда и нарастающая волна электромагнитного поля.
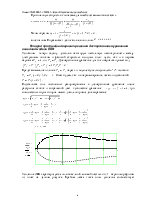
Для количественного выяснения свойств возможных типов
волн в системе "электронный поток - замедляющая линия" необходимо
составить и совместно решить систему уравнений, описывающих изменения полей,
зарядов и токов в линии и электронном потоке. Неизвестных шесть - скорость![]() ,продольное
электрическое поле E, ток в линии I, переменная
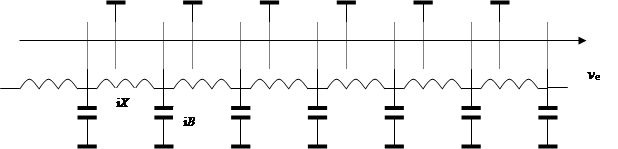
составляющая тока пучка i, напряжение в линии U, плотность заряда r. Эквивалентная схема замедляющей линии без
потерь, возбуждаемой электронным потоком.
,продольное
электрическое поле E, ток в линии I, переменная
составляющая тока пучка i, напряжение в линии U, плотность заряда r. Эквивалентная схема замедляющей линии без
потерь, возбуждаемой электронным потоком.
 |
Параметры электронного потока:
![]()
U0 - ускоряющее напряжение,
I0 - средний ток на входе в замедляющую систему.
Параметры линии:
X - реактивное сопротивление погонной индуктивности,
B - реактивная проводимость погонной емкости.
Ez - амплитуда продольного поля в линии. U,I - напряжение и ток в линии. Параметры электронного потока представим в виде суммы постоянных и переменных составляющих (переменная составляющая - амплитуда соответствующей волны):
Скорость потока: ![]()
Плотность пространственного заряда: ![]()
Ток пучка: ![]()
Продольная составляющая поля пространственного заряда:
![]()
(полагаем, что поперечные составляющие скомпенсированы фокусирующим магнитным полем), поэтому у векторных величин остаются только z-е составляющие.
Движение электронного потока описывается первыми тремя уравнениями из будущей системы шести уравнений:
(1)
![]() -
воздействие электрического поля пространственного заряда и линии
-
воздействие электрического поля пространственного заряда и линии
(2)
![]() - уравнение
Пуассона для поля пространственного заряда
- уравнение
Пуассона для поля пространственного заряда
(3)
![]() - уравнение
непрерывности потока (сохранение заряда).
- уравнение
непрерывности потока (сохранение заряда).
Ток пучка заряженных частиц через сечение пучка S и
плотность определяется как ![]() это
дает уравнение
это
дает уравнение
(6)
![]() , где знак тока i и
скорости у нас совпадает; отрицательный заряд электронов e- учитывается подстановкой
, где знак тока i и
скорости у нас совпадает; отрицательный заряд электронов e- учитывается подстановкой ![]() ,
, ![]() . Для
составления двух недостающих уравнений рассмотрим элементарный отрезок линии dz,
представленный эквивалентной схемой,
. Для
составления двух недостающих уравнений рассмотрим элементарный отрезок линии dz,
представленный эквивалентной схемой,
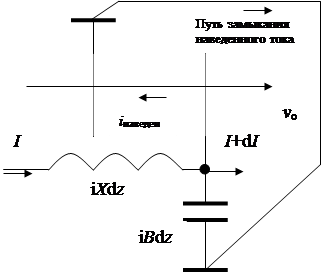 |
и напишем для него уравнение напряжений и уравнение токов. В помеченном жирной точкой узле выполняется равенство суммы токов - приходящих и уходящих:
![]() .
.
Напряжение в узле равно U, а изменение
его на коротком отрезке линии ![]() ,
таким образом получены два недостающих уравненения:
,
таким образом получены два недостающих уравненения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.