Далее, по аналогии с постоянной распространения ![]() электромагнитной
волны в холодной замедляющей системе
электромагнитной
волны в холодной замедляющей системе ![]() ,
вводятся постоянные распространения для волн электронного потока
,
вводятся постоянные распространения для волн электронного потока ![]() и плазменных
волн
и плазменных
волн ![]() , а так же,
так называемый, параметр Пирса "С", определяющий, как
увидим далее, усиление сигнала, куб которого равен:
, а так же,
так называемый, параметр Пирса "С", определяющий, как
увидим далее, усиление сигнала, куб которого равен: ![]() . Эта
величина в ЛБВ много меньше единицы - чтобы в этом убедиться, можно сопоставить
практические токи и напряжения пучка с сопротивлением связи. После этих
подстановок дисперсионное уравнение линейной модели ЛБВ принимает вид
. Эта
величина в ЛБВ много меньше единицы - чтобы в этом убедиться, можно сопоставить
практические токи и напряжения пучка с сопротивлением связи. После этих
подстановок дисперсионное уравнение линейной модели ЛБВ принимает вид ![]() .
.
Из этого уравнения определению подлежит постоянная распространения ![]() , где фазовая
скорость
, где фазовая
скорость ![]() отличается
от
отличается
от ![]() за счет
влияния пучка. Это уравнение 4-й степени - имеет 4 корня. Один из них
отрицательный, он описывает волну, движущуюся вспять.
за счет
влияния пучка. Это уравнение 4-й степени - имеет 4 корня. Один из них
отрицательный, он описывает волну, движущуюся вспять.
Здесь мы можем исследовать два простейших физически осмысленных
варианта: первый - самый простой - пренебрегая пространственным зарядом
полагаем плазменную частоту равной нулю ![]() , а
, а ![]() - пучок
электронов движется синхронно с "холодной" волной. Второй вариант
- пучок
электронов движется синхронно с "холодной" волной. Второй вариант ![]() , но
, но ![]() , хотя их
величины, все равно, полагаем очень близкими.
, хотя их
величины, все равно, полагаем очень близкими.
Пусть пространственный заряд мал,
и пучок движется синхронно с волной в холодной линии, тогда пренебрегаем
плазменной частотой ![]() ,
уравнение приобретает вид:
,
уравнение приобретает вид: ![]() ,
и при синхронизме еще и
,
и при синхронизме еще и ![]() :
:
![]() .
.
Будем искать приблизительное решение, близкое к
постоянной распространения "холодной " волны, в виде ![]() , где C<<1 - параметр Пирса, а x - неизвестное комплексное число. После
подстановки этого приближения удерживаем только члены с первой степенью "С":
, где C<<1 - параметр Пирса, а x - неизвестное комплексное число. После
подстановки этого приближения удерживаем только члены с первой степенью "С":
![]()
![]()
![]()
![]() .
.
Еще раз пренебрегая величиной Сх, имеем следующий качественный результат - Г для трех типов волн, распространяющихся попутно потоку электронов:
![]() ,
,
![]() - не затухающая быстрая волна;
- не затухающая быстрая волна;
![]() ,
,
![]() - нарастающая по экспоненте рабочая
волна;
- нарастающая по экспоненте рабочая
волна;
![]() ,
,
![]() - затухающая медленная волна. Так как все эти
три типа волн равноправны, начальным условием считаем, что входной сигнал
поделен поровну между этими типами волн, и процесс в ЛБВ является их
суперпозицией. Из полученного результата для рабочей волны уже можно написать
формулу коэффициента усиления ЛБВ в режиме слабого сигнала:
- затухающая медленная волна. Так как все эти
три типа волн равноправны, начальным условием считаем, что входной сигнал
поделен поровну между этими типами волн, и процесс в ЛБВ является их
суперпозицией. Из полученного результата для рабочей волны уже можно написать
формулу коэффициента усиления ЛБВ в режиме слабого сигнала: 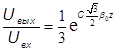 ,
где z - пройденный вдоль оси
z путь. Если длина замедляющей системы l, то в ней укладываются N
замедленных волн
,
где z - пройденный вдоль оси
z путь. Если длина замедляющей системы l, то в ней укладываются N
замедленных волн ![]() ;
; ![]() и
и
![]() ,
или
,
или ![]() Электроны
движутся быстрее электромагнитной волны, т.к электроны вносят емкостную
составляющую в распределенную емкость. Для того, чтобы электроны отдали энергию
волне, необходимо, чтобы они затормозились, но затормозиться они могут только
до фазовой скорости "холодной" волны. Таким образом, из условия
Электроны
движутся быстрее электромагнитной волны, т.к электроны вносят емкостную
составляющую в распределенную емкость. Для того, чтобы электроны отдали энергию
волне, необходимо, чтобы они затормозились, но затормозиться они могут только
до фазовой скорости "холодной" волны. Таким образом, из условия ![]() для
медленной волны мы можем оценить электронный КПД
для
медленной волны мы можем оценить электронный КПД ![]() для ЛБВ
для ЛБВ
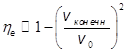 .
.
Про конечную скорость в конце замедляющей системы можно сказать
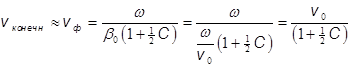 .
.
Таким образом ![]() , а постоянная Пирса может достигать величин лишь
, а постоянная Пирса может достигать величин лишь ![]()
Усложним теперь задачу, дозволив некоторую небольшую несинхронность
между электронным потоком и фазовой скоростью холодных волн: пусть, как и в
первом варианте![]() ,
но
,
но ![]() .
Дисперсионное уравнение для этого варианта примет вид
.
Дисперсионное уравнение для этого варианта примет вид
![]()
Представим малое
отличие ![]() через т.н. параметр
несинхронности "y": положив
через т.н. параметр
несинхронности "y": положив ![]() . Ответ
будем, как и в первом варианте, искать подстановкой
. Ответ
будем, как и в первом варианте, искать подстановкой ![]() .
.
Подстановка этих постоянных распространения в дисперсионное уравнение
после раскрытия скобок и сокращений дает кубическое уравнение ![]() , три
комплексных корня которых имеют довольно громоздкое выражение
, три
комплексных корня которых имеют довольно громоздкое выражение
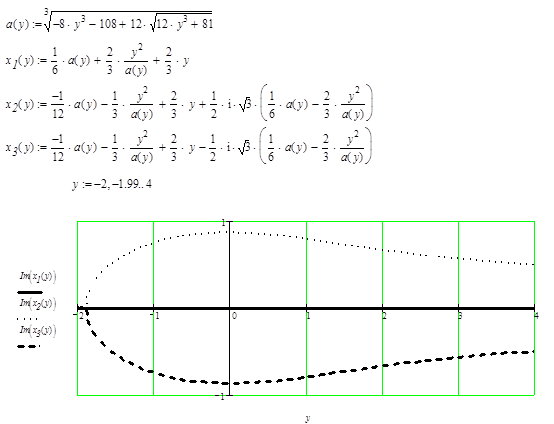
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.