Лампа бегущей волны. Принцип работы ЛБВ О-типа. Теория ЛБВ в режиме малого сигнала, страница 5

Важной особенностью замедленных волн является их непосредственная “привязанность”, “прилипание” к замедляющей системе. В пространстве возле замедляющей системы продольное поле E_z убывает с расстоянием от замедляющей системы экспоненциально, поэтому Z₀ постоянно только вдоль поверхностей, параллельных оси замедляющей системы, т.н. импедансных поверхностей. 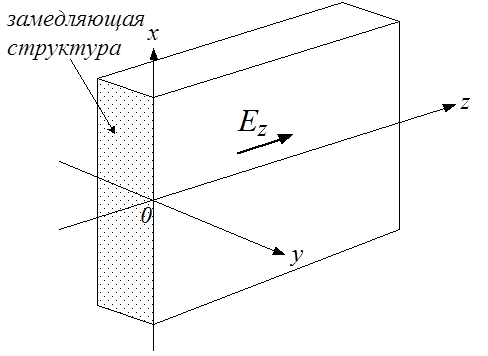Понять это можно, рассмотрев решения уравнения Гельмгольца, которому удовлетворяет электрическое поле в вакууме           на простейшем примере, изображенном на рисунке.  В бесконечной плоской стенке в плоскости x0z, вдоль оси z распространяется замедленная волна , - в этом выражении мы полагаем, что зависимость от x отсутствует, поэтому  . Подстановка выражения в уравнение Гельмгольца дает

.

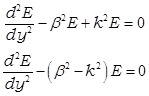Для замедленной волны , значит и, следовательно, решением для E(y) является экспонента с вещественным показателем , поскольку . При этом на границе (стенке), где . Такая ситуация физически реализуется, если полупространство   заполнено диэлектриком, в котором скорость света уменьшена в  раз, и электромагнитная волна распространяется с условием полного внутреннего отражения от стенки -  поверхности раздела сред. Электромагнитное поле при этом выступает над поверхностью диэлектрика всё дальше по мере приближения к наибольшему углу полного внутреннего отражения (при этом уменьшается до единицы коэффициент замедления волны на поверхности). Таким образом, для замедленной волны над поверхностью плоской замедляющей системы имеет физический смысл только затухающая экспонента: , . При большом замедлении , т. е. чем больше замедление , тем больше  , и тем быстрее происходит спад поля в зависимости от расстояния y. Если замедляющая система не плоская, а круглая (спираль, например), то спад поля описывается Бесселевыми функциями от мнимого аргумента (подобно тому, как обычные распространяющиеся осесимметричные волны описываются Бесселевыми функциями вещественного аргумента). На практике большое замедление реализовать диэлектриком трудно, так как при больших значениях электрической проницаемости e у диэлектриков велики потери.

Поэтому замедляющие системы в основном делаются в виде периодических структур, основными типами которых являются 1) спираль, 2) диафрагмированный волновод (цепочка связанных резонаторов), 3) гребенка 5) встречные штыри. Период структуры – минимальное расстояние p вдоль z между подобными элементами структуры – много меньше длины замедленной волны  у однородных структур, таких, как спираль, и порядка длины волны у неоднородных замедляющих систем. В однородных системах мгновенная картина поля практически синусоидальна от z, в неоднородных полях существенно несинусоидально, его можно изобразить ступенчатой функцией. В зазоре каждой ячейки периодичности поле бегущей волны отлично от поля зазора предыдущей лишь на фазовый угол : . Функция  не является периодической, , поэтому она на периоде структуры не может быть разложена в ряд Фурье обычным способом, но по периоду структуры можно ввести новую функцию , в которой учтен сдвиг фазы на ячейку; тогда 

, эта функция уже периодична, и ее можно разложить в ряд Фурье по периоду структуры на “пространственные гармоники”:,

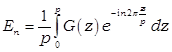
Этим способом мы представим поле в виде суммы волн с разными постоянными распространения, но с общей фиксированной частотой .  Вернемся назад от функции G к функции E ,  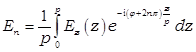- амплитуда n-й гармоники. Постоянная распространения  для n-й гармоники зависит от сдвига фазы на ячейку:

, где . В поперечном от замедляющей структуры направлении показатель пространственного затухания замедленной волны  возрастает с номером гармоники, и высшие гармоники более всего “прилипают” к замедляющей системе, поэтому используют в основном нулевую и ± первую гармоники. Для работы ЛБВ необходим синхронизм: , то есть выбор коэффициента замедления связан с выбором энергии электронов в пучке – с ускоряющим напряжением: 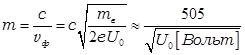. У маломощных ЛБВ напряжение ускорения порядка киловольта , у очень мощных ЛБВ напряжение ускорения порядка пятидесяти киловольт: . И условие синхронизма состоит в том, что скорость электронов должна совпасть со скоростью одной из пространственных гармоник; скорость движения уплотнений электронного потока совпадает со скоростью электронов (при пренебрежении влиянием пространственного заряда в пучке) и  .