(4)
![]()
(5)
![]() .
.
Можно ввести волновое сопротивление для продольного поля ![]() ,
характеризующее отношение продольных составляющих тока и напряжение в месте
пролета пучка. Оно имеет смысл сопротивления связи, через которое ток пучка
взаимодействует с волной в линии. Постоянная распространения волны в
замедляющей линии
,
характеризующее отношение продольных составляющих тока и напряжение в месте
пролета пучка. Оно имеет смысл сопротивления связи, через которое ток пучка
взаимодействует с волной в линии. Постоянная распространения волны в
замедляющей линии ![]() ,
где
,
где ![]() - фазовая
скорость волны в замедляющей системе;
- фазовая
скорость волны в замедляющей системе; ![]() . Эта
постоянная распространения дает решение для волны в отсутствии пучка.
. Эта
постоянная распространения дает решение для волны в отсутствии пучка.
Решение этой системы уравнений будем искать при следующих упрощениях:
1.
Линейное приближение, т.е.
![]() и
и ![]() -
малые колебания.
-
малые колебания.
2. Одномерная модель.
Чтобы начисто переписать подготовленную к решению систему уравнений, разложим полную производную скорости в первом уравнении
![]() ,
и учитывая линейное приближение
,
и учитывая линейное приближение ![]() ,
,
![]() , можно
записать упрощенные уравнения для переменных величин, учитывая что постоянные
составляющие исчезают:
, можно
записать упрощенные уравнения для переменных величин, учитывая что постоянные
составляющие исчезают:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4) здесь проведена замена iнавед=-i
(4) здесь проведена замена iнавед=-i
![]() (5)
(5)
![]() (6)
(6)
Решением линейных дифференциальных уравнений являются
волны, распространяющиеся вдоль z, они представлятся экспонентами вида ![]() , где
, где ![]() - множество
из шести неизвестных амплитуд соответствующих величин.
- множество
из шести неизвестных амплитуд соответствующих величин.
Подстановка экспонент указанного вида эквивалентна
замене ![]() и
и ![]() ,
, ![]() . Таким
образом мы получаем Фурье - образ системы линейных дифференциальных уравнений в
виде системы шести однородных алгебраических уравнений для данных шести
неизвестных:
. Таким
образом мы получаем Фурье - образ системы линейных дифференциальных уравнений в
виде системы шести однородных алгебраических уравнений для данных шести
неизвестных:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6).
(6).
Первые три уравнения, и шестое описывают
взаимодействие электронного потока, третье и четвертое - поля в линии. Их можно
записать в виде равенства нулю матрицы коэффициентов М, умноженной на вектор V-
столбец из перечисленных шести неизвестных ![]() : M×V=0
: M×V=0
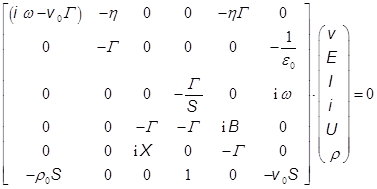
Однородная система имеет нетривиальные решения при равенстве нулю ее определителя (детерминанта) detM=0. Частота w нам дана усиливаемым сигналом, надо найти обнуляющую детерминант постоянную распространения Г. Детерминант М имеет выражение:
![]()
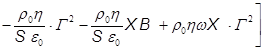 .
.
Тривиальный корень Г=0 нас не интересует, а в скобках остается уравнение 4-й степени, сложное для анализа в таком виде без дополнительных упрощений и добавочных физических понятий.
Из первых трех и шестого уравнения получается
выражение для переменной составляющей тока пучка. Из уравнения (1) выражаем
переменную скорость, подставив выражение электрического поля пространственного
заряда ![]() из
уравнения (2):
из
уравнения (2): 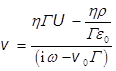 ; а
из уравнений (3) выражение
; а
из уравнений (3) выражение ![]() и
подставляем его в уравнение (6) вместе с последним выражением переменной составляющей
скорости (6) , а в выражении скорости
тоже заменяем r на его выражение из уравнения (3)
и
подставляем его в уравнение (6) вместе с последним выражением переменной составляющей
скорости (6) , а в выражении скорости
тоже заменяем r на его выражение из уравнения (3)
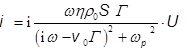 , где
, где 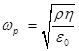 - плазменная
частота. Независимо от этого мы можем получить выражение для i из
уравнений (4) и (5) путем исключения тока в линии I:
- плазменная
частота. Независимо от этого мы можем получить выражение для i из
уравнений (4) и (5) путем исключения тока в линии I:
![]() ;
;
![]() ;
; ![]() .
.
Вводя обозначение постоянной распространения в
"холодной линии" ![]() ,
приравниваем i=i и,
сократив с двух сторон множитель U получаем дисперсионное уравнение:
,
приравниваем i=i и,
сократив с двух сторон множитель U получаем дисперсионное уравнение: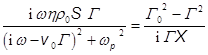 . Для
дальнейших преобразований наружного вида этого уравнения учтем три соотношения:
во первых, соотношение между индуктивной погонной реактивностью, волновым
сопротивлением и постоянной распространения
. Для
дальнейших преобразований наружного вида этого уравнения учтем три соотношения:
во первых, соотношение между индуктивной погонной реактивностью, волновым
сопротивлением и постоянной распространения![]() , во вторых
определение полного тока пучка
, во вторых
определение полного тока пучка ![]() ,
и, в третьих, соотношение между скоростью и энергией нерелятивистского
электрона
,
и, в третьих, соотношение между скоростью и энергией нерелятивистского
электрона ![]() . После этих
подстановок дисперсионное уравнение имеет вид:
. После этих
подстановок дисперсионное уравнение имеет вид:
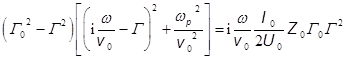 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.