Лампа бегущей волны. Принцип работы ЛБВ О-типа. Теория ЛБВ в режиме малого сигнала, страница 6

Ввод управляющего сигнала в ЛБВ и вывод энергии из ЛБВ

Обычные требования: КСВН < 1.5 в рабочей полосе частот, составляющей . Обычно волновое сопротивление подключенных к ЛБВ внешних линий больше волнового сопротивления замедляющей линии , поэтому требуются на входе и выходе согласующие устройства, каковыми могут быть 1) волноводно-спиральный переход (на малых мощностях), 2) резонатор (на больших мощностях), 3) Связанные спирали: внешние спирали с распределенной связью, расположенные поверх спиральной замедляющей системы, подобно линиям ответвителя с распределенной связью.

Антипаразитный балластный поглотитель СВЧ

Назначение – устранить самовозбуждение автоколебаний в ЛБВ, возникающее из-за отражения волны от вывода и ввода энергии. Поглотитель ставится в середине или немного ближе к началу замедляющей системы. Он поглощает практически всю мощность электромагнитных волн, бегущих в замедляющей системе. Это, по существу, разрыв линии, причем с хорошим согласованием с обеих сторон – и со стороны входа, и со стороны выхода  – КСВН<1.02, однако лампа сохраняет работоспособность, так как усиливаемый сигнал уже вызвал модуляцию электронного пучка, и именно электронный пучок переносит усиливаемый сигнал сквозь зону поглотителя.

Фокусировка магнитным полем

Рассмотрим электрон  с зарядом e < 0,  движущийся в аксиально - симметричном магнитном поле .

Уравнения движения для азимутальной составляющей скорости  , исходя из выражения для скорости изменения момента количества движения, можно записать в виде

Магнитный поток, пронизывающий площадь, охваченную окружностью с радиусом r относительно оси симметрии равен интегралу . Если электрон перемещается из точки с координатами  в точку с координатами  , то скорость изменения потока, охваченного этой окружностью можно найти из выражения  в цилиндрических координатах: . Приращение потока, охваченного окружностью равно

.

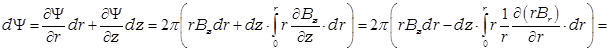
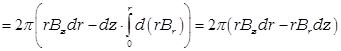Подставляя радиальную и продольную скорость получаем скорость изменения охваченного окружностью потока:. Ее можно подставить в правую часть уравнения азимутального движения:. Интегрируя уравнение с начальными условиями , где y₀ - поток, охваченный окружностью радиуса влета с нулевой азимутальной скоростью (электроны покидают катод с нулевой азимутальной скоростью), получаем т.н. уравнение Буша: .

Далее можно рассмотреть два крайних случая: первый – тривиальный – если катод находится в магнитном поле, остающемся постоянным на всем прямолинейном пути электронов, их траектории остаются прямолинейными и азимутального движения не возникает. При этом усиление магнитного поля уменьшает радиус Ларморовских окружностей и препятствует, таким образом, поперечному движению электронов, летящих по спиралеобразным траекториям. Другой вариант – катод находится вне магнитного поля фокусирующей системы, и электроны влетают в магнитное поле с условиями . Внутри соленоида фокусирующей системы, как показано на рисунке, практически однородное магнитное поле  B_z: . Соответствующая угловая скорость азимутального движения  называется Ларморовской частотой и составляет ровно половину циклотронной частоты: . Все частицы при этом, хотя и выписывают спиралеобразные траектории, касающиеся оси симметрии, как показано на рисунке, вращаются вместе с пучком как единое целое, с постоянной угловой скоростью.

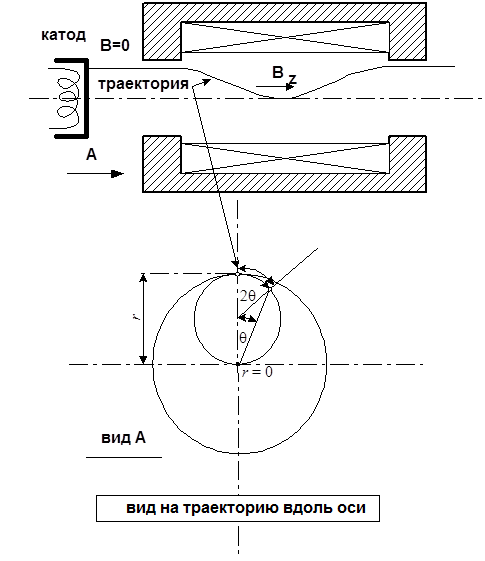
Попытаемся получить условие для стационарного цилиндрического пучка с постоянной по радиусу и длине плотностью заряда (и тока). Для этого надо уравнять три силы действующие на каждый электрон: силу Лоренца, центробежную силу и силу Кулоновского отталкивания от цилиндрического объемного заряда пучка:

 . Далее, сократив радиус, получаем условие равновесия сил, не зависящее от радиуса: . Подставим выражение : путем сокращения получаем выражение для равновесного магнитного поля (поля Бриллюэна) при котором внешняя граница пучка становится прямой линией: 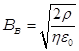. На практике продольное поле делают немного (в 1.3, 1.6 раза) сильнее, при этом наблюдаются небольшие, но приемлемые по величине, пульсации границы пучка.