Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Методы описания воздействия ледяного покрова на сооружения шельфа), страница 7

Ясно, что для достаточно большого интервала времени N @2lT.

Пусть {^RR(t)} - множество возможных значений внешнего возмущения. Скорость судна, вызванная случайной силой ^RR(t), также будет случайной функцией времени ^RV(t). Тогда дифференциальное уравнение движения судна водоизмещением D по прямому курсу запишется так [26]:

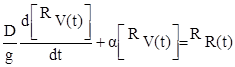                                         (29)

где индекс R соответствует к-той реализации случайного процесса.

Правая часть уравнения (29) при установившемся режиме движения судна является стационарной случайной функцией времени. В первом приближении ее можно представить следующим образом:

,    при tj£ t ³t_j+1 (j=0, ±1)                                    (30)

Случайный процесс (30) описывает величину случайного импульса силы, действующей на судно при движении по прямой в статистически однородных ледовых условиях.

Как уже отмечалось, рассматриваемый процесс является пуассоновым. Спектральная плотность такого процесса определяется по формуле [25]

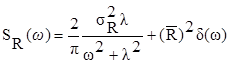                                            (31)

Корреляционная функция для R(t) будет иметь вид

                                                (32)

Дисперсия силы прямого ледового сопротивления s_R² не равна нулю даже в идеально однородных сплошных льдах, т. к. ломка льда происходит по длине борта на случайных участках, имеющих различный наклон. При этом контактные усилия будут зависеть от случайной координаты точек взаимодействия. Дисперсию s_R² здесь можно оценить, используя трехточечную статическую схему ломки. В этом случае рассматривается такое взаимодействие судна со льдом, когда одновременно осуществляется соприкосновение и ломка льда в трех точках. Этот треугольник определяет равновесное статически определимое положение судна. точка 1 есть точка касания форштевня. Точки 2 и 3 располагаются по бортам судна симметрично его диаметральной плоскости. В этих точках действуют контактные усилия R_N, направленные по нормали к борту судна, а также пропорциональные им силы трения, направленные по касательной к борту. Найдем проекцию контактных усилий с обоих бортов на ось X с учетом сил трения:

                                                   (33)

где l- направляющий косинус нормали к борту судна; a - угол наклона к диаметральной плоскости касательной к ватерлинии; f_t - коэффициент трения борта судна о лед.

Под действием вертикальной составляющей контактного усилия Rz=R_Nsin b^/ лед ломается. Здесь b^/ - угол наклона борта к вертикали в точке контакта. Полагаем, что в контакт с бортом в точках 2 и 3 входят полубесконечные ледяные пластины. Для ломки таких пластин требуется усилие [24]

                                                             (34)

где h - толщина льда; s_p - предел прочности льда на изгиб.

В точке 1 контакта форштевня со льдом действует нормальное к фортштевню усилие R_N^/ и пропорциональная ему сила трения R_T^/=f_T^/×R_N^/.

Приведенный коэффициент трения f_T^/ определяется по следующей формуле [27]:

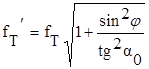                                                      (35)

где j - угол наклона форштевня к горизонту; a₀ - угол входа носовой ветви ватерлинии. Проекция этих усилий на ось х будет

                                                   (36)

Для определения вертикальной составляющей контактного усилия R'z рассмотрим ломку бесконечной пластины с клинообразным вырезом, имеющим угол раствора 2a₀. В этом случае [24]:

                                                 (37)

составим уравнение статического равновесия судна в проекции на ось x. Полагая контактные усилия равными разрушающим лед, величину силы прямого ледового сопротивления определим по формуле

,                                                  (38)

где

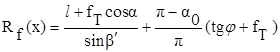                                        (39)

где a₀ - безразмерный коэффициент, характеризующий форму корпуса судна.