где Fix - проекция на ось OX давления корпуса на лед в i-той точке контакта, приходящегося на единицу площади контакта (в частном случае на единицу длины); dxi - возможное перемещение i-той точки контакта корпуса со льдом вдоль оси OX при возможном перемещении судна на dx; Pel - тяга винтов с учетом особенностей их работы во льду.
Пренебрегая инерционными составляющими и считая, что поле льда деформируется упруго вплоть до разрушения, для нормальных давлений на лед запишем
![]() (23)
(23)
где а - коэффициент пропорциональности; eni- перемещение кромки льда в i-той точке контакта по направлению внешней нормали к корпусу.
Учитывая трение корпуса о лед и силы, возникающие на форштевне определяют проекции давлений на кромку льда.
Далее получают раcсчeтные формулы для определения давлений при взаимодействии корпуса ледокола с ледяным полем. В качестве примера расчета по предлагаемым формулам на графиках [19] приведены значения давлений взаимодействия корпуса речного ледокола, предполагая, что контакт происходит по всей длине носового заострения Ln, а коэффициент трения ftr =0,15.
Далее авторы проводили экспериментальное определение напряженного состояния ледяного покрова. При принятых допущениях: ледяное поле считается однородной изотропной (трансверсально-изотропной) пластинкой постоянной толщины и бесконечных размеров, лежащей на упругом основании гидравлического типа. Уравнение изгиба поля имеет вид
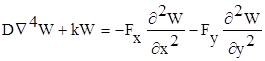 , (27)
, (27)
где W=W(x,y) - функция, описывающая прогиб льда; D=Et3/12(1-m2) - цилиндрическая жесткость пластины толщиной t с модулем Юнга Е и коэффициентом Пуассона m; k - коэффициент жесткости упругого основания; Fx, Fy - усилия, действующие в срединной плоскости.
Полученные экспериментальные данные авторы предлагают использовать для анализа роли отдельных составляющих давлений при взаимодействии корпуса ледокола со льдом и теоретических методах расчета напряженного состояния поля льда.
При движении в сплошных ледяных полях судно испытывает противодействие, складывающееся из сил сопротивления воды и сил ледового сопротивления. Предельная толщина сплошного льда, которую может преодолеть судно непрерывным ходом, является одним из главнейших показателей ледокольных качеств судна. Наряду с определением максимальной толщины льда, преодолеваемой судном, необходимо произвести исследование устойчивости его движения в данных условиях (т.е. определить время непрерывного движения судна во льдах) [43].
Д.Е. Хейсин предлагает сравнительно простую расчетную схему оценки усилий ледового сопротивления движению судна в сплошных льдах. При этом используются вероятностные методы анализа, а взаимодействие корпуса со льдом рассматривается как случайный процесс. Сопротивление движению судна в основном определяется так называемым ледовым сопротивлением, не зависящим от скорости [24].
Силу ледового сопротивления движению судна во льдах Rb Д.Е. Хейсин представляет как результат последовательно приложенных к корпусу ударных импульсов, противодействующих движению. Для установившихся режимов движения судна этот случайный процесс является стационарным и эргодическим.
Счетное множество дискретных внешних воздействий образует упорядоченный временной ряд. Такой ряд можно получить, разбив случайным образом бесконечную временную ось бесконечной последовательностью точек tj на интервалы конечной длины Dtj=tj+1-tj.
Если взять произвольный интервал времени (-Т,Т), то число точек N, попавших в этот интервал, будет случайной величиной. Как показали эксперименты [25], число N, т.е. количество ударов, подчиняется закону распределения Пуассона
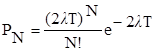 (28)
(28)
Для стационарных режимов средняя плотность распределения ударных импульсов во времени l постоянна. Эта величина также определялась экспериментально [25].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.