Ледовая нагрузка, действующая на конструкции транспортных судов, определяется совокупностью многих случайных параметров (свойства льда, толщина и геометрия кромки ледяного покрова, скорость судна и т.д.) Законы распределения этих случайных величин в настоящее время не установлены.
Данных по свойствам льда, толщинам и сплоченности ледяного покрова недостаточно для построения вероятностной модели ледяного покрова.
Таким образом, для определения ледовой нагрузки остается два пути: либо статистическая обработка опытных данных, либо путь, основанный на построении некоторой теоретической модели взаимодействия корпуса судна со льдом. Второй подход нашел широкое приложение в практике.
Ясно, что чем лучше теоретическая модель описывает физические процессы, происходящие при взаимодействии корпуса со льдом, тем более универсальной и гибкой будет методика определения ледовой нагрузки.
Усилия взаимодействия корпуса судна со льдом не могут превзойти нагрузки, разрушающей лед. Этот тезис был выдвинут А.И. Масловым [17] более 40 лет назад и явился основополагающим для определения нагрузки на конструкции ледового пояса, как для судов, так и для гидротехнических сооружений шельфа.
При контакте борта судна со льдом происходит статическое или динамическое раздробление кромки бортом, а также возможно разрушение ледяного покрова от изгиба на потерю устойчивости. Следовательно, для построения теоретической модели нужно решать две задачи [19]:
1. о несущей способности ледяного покрова;
2. о раздроблении льда твердым телом, что актуально и для гидротехников.
В.И. Каштелян предлагает оценивать несущую способность ледяного покрова по формуле вида [18]:
![]() (14)
(14)
где Pp - вертикальная компонента суммарной силы; k - численный коэффициент; sр - предел прочности льда на изгиб; H - толщина льда.
Для определения контактных усилий используется гидродинамическая модель удара твердого тела о лед [20]:
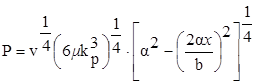 (15)
(15)
где v - скорость внедрения тела в лед; (6mkp3)1/4 - измеритель динамической прочности льда (см. [20]); b - высота волн зоны контакта по борту; x - координата по высоте зоны контакта; a>1 - коэффициент, учитывающий сколы по краям зоны контакта.
Выражения для давления p, высоты распределения ледовой нагрузки b и суммарной силы P следуют из решения уравнения движения судна в направлении удара. Причем их можно построить или в зависимости от глубины внедрения борта в лед, или как функцию относительной скорости внедрения k=v/v01 (v - скорость внедрения, v0 - скорость поступательного движения до удара; l -коэффициент приведения скорости к направлению удара). Вторая форма удобнее, так как выражения для ледовой нагрузки согласуются с решением для коэффициентов приведения [21].
Приравнивая вертикальную компоненту суммарной силы нагрузке, разрушающей ледяной покров определяют оптимальное значение kmin (в случае, если Pp>Psin b , где b - угол наклона шпангоута, k=0).
Зная kmin вычисляют максимальные значения p и b, т.е. ледовую нагрузку.
Можно решить и обратную задачу: по известной прочности конструкций ледового пояса определить допустимые для данного судна условия ледового плавания.
Обратная задача для гидротехников не представляет интереса, но представляет интерес для судостроителей с целью определения оптимальной формы обводов судна, что было выполнено В.А. Курдимовым [19].
В.А. Зуев, С.В. Кошкин [23] предложили экспериментальную модель определения напряженного состояния ледяного поля при движении ледокола.
Для определения давлений на лед при движении ледокола с малой скоростью применим принцип возможных перемещений, согласно которому при поступательном движении судна получают
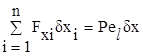 (22)
(22)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.