Н.Г. Храпатый и В.Г. Цуприк предложили расчет силы удара льдин об отдельную опору, основанный на энергетическом подходе к расчету [32]. Авторы отмечают, что слабая изученность процессов удара и развития контактных явлений при соударении льдины с сооружением не позволяет в настоящее время получить все параметры, характеризующие контакт, путем прямого расчета. При расчете ледовой нагрузки контактное давление у кромки льдины с сооружением обычно принимается равным пределу прочности льда на раздробление (смятие) или на сжатие - в зависимости от типа конструкции и условий работы сооружения.
В любом случае при ударе льдины о сооружение, имеющее небольшие размеры в плане, это сооружение внедрится в лед. При этом разрушение льда в зоне контакта сопровождается отколами, дроблением осколков, взаимным уменьшением площади контакта вследствие откола льда. Таким образом, за счет превышения величины контактных напряжений над временным сопротивлением льда разрушению сооружение будет внедряться в лед, при этом опора или остановит льдину, или прорежет ее до определенной глубины, после чего льдина расколется[33].
Для опоры, имеющей цилиндрическое очертание в плане и радиусом r, рабочую площадь соприкосновения с льдиной можно записать в виде
![]() ,
(55)
,
(55)
где h - величина (стрелка) внедрения; Н -толщина льда. В этом случае дифференциальное уравнение движения льдины
![]() ,
(56)
,
(56)
где М -масса льдины; Rp - сопротивление льда разрушению. Второе слагаемое уравнения (56) определяет величину контактной силы
![]() (57)
(57)
максимум которой определяется из решения уравнения (56) как
![]() (58)
(58)
Здесь V, W - скорость движения и площадь льдины; r - плотность льда.
В свою очередь, глубина внедрения опоры в лед определяется из уравнения (56)
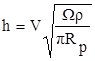 (59)
(59)
Формула (58) не отличается по виду и входящим в нее параметрам от рекомендаций СНиП [1], где предел использования этой формулы устанавливается скоростью движения льдины (поля) в 1 м/с и значением Rp, пропорциональным пределу прочности льда на сжатие. Но в натурных условиях эксплуатации и строительства гидротехнических сооружений скорости движения отдельных льдин достигают величины в 1,5-2 раза выше этого предела[35,36]. Экспериментальные исследования и результаты натурных наблюдений [34,36,37] указывают на зависимость величины контактных давлений от скорости соударения льдины с преградой, формы опоры в плане и ряда других факторов. Но из-за слабой изученности перечисленные обстоятельства пока не поддаются полному учету.
Затем авторы останавливаются на вопросе разрушения льда при местных контактных воздействиях, где они предлагают оценить сопротивляемость льда разрушению удельной энергией дробления льда, т.е. мерой затрат энергии движения льдины на единицу массы разрушенного материала в объеме контактной каверны. При этом движение льдины будет продолжаться, пока контактное давление R будет превосходить предельное значение давления Rпр, необходимое для разрушения льда:
![]() (60)
(60)
Здесь Vk - критическая скорость разрушения льда, которая определяет величину удельной энергии механического разрушения льда e = 0,5Vk2 и для морского льда находится в пределах 0,8-1,0 и 0,5-1,6 м/с для пресного льда.
Таким образом, критическое давление, необходимое для разрушения льда и продвижения льдины,
![]() (61)
(61)
Удельная энергия механического дробления определялась по соотношению [7]
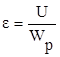 (62)
(62)
Далее в статье приводятся некоторые результаты исследований.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.